Контрольная работа: Алгебра и начало анализа
№8.Опр . Отношение катета, противолежащего острому углу прямоугольного треугольника, к катету, прилежащему к этому углу, называется тангенсом (обозначается tg ![]() ).
).
- область определения - множество всех действительных чисел, кроме чисел вида
 ;
; - множество значений - вся числовая прямая;
- функция нечетная: tg(-x) = -tg(x) для всех х из области определения;
- функция периодическая с наименьшим положительным периодом
 ;
; - tg(x) = 0 при х =
 ;
; - tg(x) > 0 для всех
 ;
; - tg(x) < 0 для всех
 ;
; - функция возрастает на
 .
.

№9.Опр . Отношение катета, прилежащего острому углу прямоугольного треугольника, к катету, противолежащему к этому углу, называется котангенсом (обозначается ctg ![]() )
)
- область определения - множество всех действительных чисел, кроме чисел вида
 ;
; - множество значений - вся числовая прямая;
- функция нечетная: ctg(-x) = -ctg(x) для всех х из области определения;
- функция периодическая с наименьшим положительным периодом
 ;
; - ctg(x) = 0 при x =
 ;
; - ctg(x) > 0 для всех
 ;
; - ctg(x) < 0 для всех
 ;
; - функция убывает на
 .
.

Ответ № 10
- Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией.
- Из определения арифметической прогрессии следует, что разность между любым ее членом и ему предшествующим равна одному и тому же числу, т. е. а2 - а1 = а3 - а2 = ... = ak - ak-1 = ... . Это число называется разностью арифметической прогрессии и обычно обозначается буквой d .
- Для того чтобы задать арифметическую прогрессию (аn ), достаточно знать ее первый член а1 и разность d .
- Если разность арифметической прогрессии - положительное число, то такая прогрессия является возрастающей; если отрицательное число, то убывающей. Если разность арифметической прогрессии равна нулю, то все ее члены равны между собой и прогрессия является постоянной последовательностью.
- Характеристическое свойство арифметической прогрессии. Последовательность (аn) является арифметической прогрессией тогда и только тогда, когда любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, т. е.
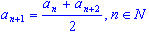 (1)
(1) - Формула n-го члена арифметической прогрессии имеет вид: an = a1 + d(n-1) . (2)
- Формула суммы n первых членов арифметической прогрессии имеет вид:
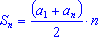 (3)
(3) - Если в формулу (3) подставить вместо аn его выражение по формуле (2), то получим соотношение
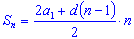
- Из определения разности арифметической прогрессии следует, что a1 + an = a2 + an-1 = ..., т. е. сумма членов, равноудаленных от концов прогрессии, есть величина постоянная.
Ответ № 11
- Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией.
- Из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е. b2 :b1 = b3 :b2 = ... = bn :bn-1 = bn+1 :bn = ... . Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q .
- Для того, чтобы задать геометрическую прогрессию (bn ), достаточно знать ее первый член b1 и знаменатель q .
- Если q > 0 (
 ), то прогрессия является монотонной последовательностью. Пусть, например, b1 = -2, q = 3, тогда геометрическая прогрессия -2, -6, -18, ... есть монотонно убывающая последовательность. Если q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.
), то прогрессия является монотонной последовательностью. Пусть, например, b1 = -2, q = 3, тогда геометрическая прогрессия -2, -6, -18, ... есть монотонно убывающая последовательность. Если q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью. - Характеристическое свойство геометрической прогрессии. Последовательность (bn ) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е.
 (1)
(1) - Формула n-го члена геометрической прогрессии имеет вид:
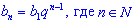 (2)
(2) - Формула суммы п первых членов геометрической прогрессии имеет вид:
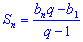 ,
,  (3)
(3) - Если в формулу (3) подставить вместо bn его выражение по формуле (2), то получится соот-ношение.
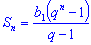 ,
,  (4)
(4) - Из определения знаменателя геометрической прогрессии следует, что b1 bn = b2 bn-1 = …, т.е. произведение членов, равноотстоящих от концов прогрессии, есть величина постоянная.
Сумма бесконечной геометрической прогрессии при ![]()
- Пусть (xn ) - геометрическая прогрессия со знаменателем q , где
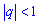 и
и 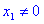 . Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию
. Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию 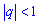 , называется предел суммы n первых ее членов при
, называется предел суммы n первых ее членов при 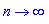 .
. - Обозначим сумму бесконечной геометрической прогрессии через S . Тогда верна формула
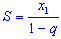 .
.
№ 12
Решение тригонометрических уравнений вида sin(x) = a
- формула для корней уравнения sin(x) = a, где
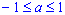 , имеет вид:
, имеет вид: 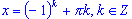
Частные случаи: - sin(x) = 0, x =

- sin(x) = 1, x =
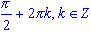
- sin(x) = -1, x =
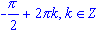
- формула для корней уравнения sin2 (x) = a, где
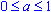 , имеет вид: x=
, имеет вид: x= 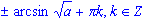
Решение тригонометрических неравенств вида sin(x) > a, sin(x) < a
- Неравенства, содержащие переменную только под знаком тригонометрической функции, называются тригонометрическими.
- При решении тригонометрических неравенств используют свойство монотонности триго-нометрических функций, а также промежутки их знакопостоянства.
- Для решения простейших тригонометрических неравенств вида sin(x) > a (sin(x) < а) используют единичную окружность или график функции y = sin(x).
sin(x) = 0 если х = ;
;
sin(x) = -1, если x =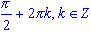 >;
>;
sin(x) > 0, если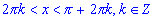 ;
;
sin(x) < 0, если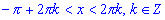 .
.
Ответ № 13
Решение тригонометрического уравнения cos(x) = a
- Формула для корней уравнения cos(x) = a, где
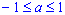 , имеет вид:
, имеет вид: 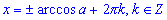 .
. - Частные случаи:
cos(x) = 1, x =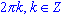 ;
;
cos(x) = 0, ;
;
cos(x) = -1, x =
- Формула для корней уравнения cos2 (x) = a, где
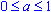 , имеет вид:
, имеет вид: 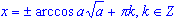 .
.
Решение тригонометрических неравенств вида cos(x) > a, cos(x) < a
- Для решения простейших тригонометрических неравенств вида cos(x) > a, cos(x) < a используют единичную окружность или график функции y = cos(x);
- Важным моментом является знание, что:
cos(x) = 0, если ;
;
cos(x) = -1, если x = ;
;
cos(x) = 1, если x =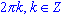 ;
;
cos(x) > 0, если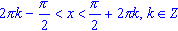 ;
;
cos(x) > 0, если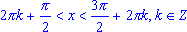 .
.
№ 14
Решение тригонометрического уравнения tg(x) = a
- Формула для корней уравнения tg(x) = a имеет вид:
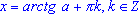 .
. - Частные случаи:
tg(x) = 0, x = ;
;
tg(x) = 1,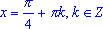 ;
;
tg(x) = -1,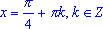 .
. - Формула для корней уравнения tg2 (x) = a, где
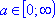 , имеет вид:
, имеет вид: 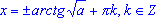
Решение тригонометрических неравенств вида tg(x) > a, tg(x) < a
- Для решения простейших тригонометрических неравенств вида tg(x) > a, tg(x) < a используют единичную окружность или график функции y = tg(x).
- Важно знать, что:
tg(x) > 0, если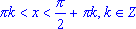 ;
;
tg(x) < 0, если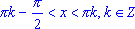 ;
;
Тангенс не существует, если .
.
№ 15
- Формулами приведения называются соотношения, с помощью которых значения тригонометрических функций аргументов
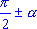 ,
,  ,
, 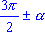 ,
,  , выражаются через значения sin
, выражаются через значения sin  , cos
, cos  , tg
, tg  и ctg
и ctg  .
. - Все формулы приведения можно свести в следующую таблицу:
| Функция | Аргумент | |||||||
|
|
|
|
|
|
|
|
| |
| sin | cos | cos | sin | -sin | -cos | -cos | -sin | sin |
| cos | sin | -sin | -cos | -cos | -sin | sin | cos | cos |
| tg | ctg | -ctg | -tg | tg | ctg | -ctg | -tg | tg |
| ctg | tg | -tg | -ctg | ctg | tg | -tg | -ctg | ctg |
- Для облегчения запоминания приведенных формул нужно использовать следующие правила:
a) при переходе от функций углов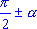 ,
, 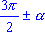 к функциям угла
к функциям угла  название функции изменяют: синус на косинус, тангенс на котангенс и наоборот;
название функции изменяют: синус на косинус, тангенс на котангенс и наоборот;
при переходе от функций углов ,
,  к функциям угла
к функциям угла  название функции сохраняют;
название функции сохраняют;
б) считая острым углом (т. е.
острым углом (т. е. 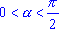 ), перед функцией угла
), перед функцией угла  ставят такой знак, какой имеет приводимая функ-ция углов
ставят такой знак, какой имеет приводимая функ-ция углов 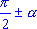 ,
,  ,
, 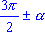 .
.
Все вышеприведенные формулы можно получить, пользуясь следующим правилом:
Любая тригонометрическая функция угла 90°n + ![]() по абсолютной величине равна той же функции угла
по абсолютной величине равна той же функции угла ![]() , если число n - четное, и дополнительной функции, если число n - нечетное. При этом, если функция угла 90°n +
, если число n - четное, и дополнительной функции, если число n - нечетное. При этом, если функция угла 90°n + ![]() . положительна, когда
. положительна, когда ![]() - острый угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
- острый угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
№ 16
- Формулы косинуса суммы и разности двух аргументов:
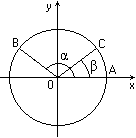
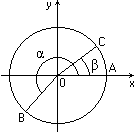
Рис.1 Рис.2
Повернем радиус ОА, равный R, около точки О на угол и на угол
и на угол  (рис.1). Получим радиусы ОВ и ОС. Найдем скалярное произведение векторов
(рис.1). Получим радиусы ОВ и ОС. Найдем скалярное произведение векторов  и
и  . Пусть координаты точки В равны х1 и y1, координаты точки С равны х2 и y2. Эти же координаты имеют соответственно и векторы
. Пусть координаты точки В равны х1 и y1, координаты точки С равны х2 и y2. Эти же координаты имеют соответственно и векторы  и
и  . По определению скалярного произведения векторов:
. По определению скалярного произведения векторов:


 = х1 х2 + y1 y2 . (1)
= х1 х2 + y1 y2 . (1)
Выразим скалярное произведение

 через тригонометрические функции углов
через тригонометрические функции углов  и
и  . Из определения косинуса и синуса следует, что
. Из определения косинуса и синуса следует, что
х1 = R cos , y1 = R sin
, y1 = R sin  , х2 = R cos
, х2 = R cos  , y2 = R sin
, y2 = R sin  .
.
Подставив значения х1 , х2 , y1 , y2 в правую часть равенства (1), получим:


 = R2 cos
= R2 cos cos
cos + R2 sin
+ R2 sin sin
sin = R2 (cos
= R2 (cos cos
cos + sin
+ sin sin
sin ).
).
С другой стороны, по теореме о скалярном произведении векторовимеем:


 =
= 
 cos
cos  BOC = R2 cos
BOC = R2 cos  BOC.
BOC.
Угол ВОС между векторами и
и  может быть равен
может быть равен  -
-  (рис.1),
(рис.1),  - (
- ( -
-  ) (рис.2) либо может отличаться от этих значений на целое число оборотов. В любом из этих случаев cos
) (рис.2) либо может отличаться от этих значений на целое число оборотов. В любом из этих случаев cos  BOC = cos (
BOC = cos ( -
-  ). Поэтому
). Поэтому


 = R2 cos (
= R2 cos ( -
-  ).
).
Т.к.

 равно также R2 (cos
равно также R2 (cos cos
cos + sin
+ sin sin
sin ), то
), то
cos( -
-  ) = cos
) = cos cos
cos + sin
+ sin sin
sin .
.
cos( +
+  ) = cos(
) = cos( - (-
- (- )) = cos
)) = cos cos(-
cos(- ) + sin
) + sin sin(-
sin(- ) = cos
) = cos cos
cos - sin
- sin sin
sin .
.
Значит,
cos( +
+  ) = cos
) = cos cos
cos - sin
- sin sin
sin .
. - Формулы синуса суммы и разности двух аргументов:
sin( +
+  ) = cos(
) = cos(  /2 - (
/2 - ( +
+  )) = cos((
)) = cos((  /2 -
/2 -  ) -
) -  ) = cos(
) = cos(  /2 -
/2 -  ) cos
) cos + sin(
+ sin(  /2 -
/2 -  ) sin
) sin = sin
= sin cos
cos + cos
+ cos sin
sin .
.
Значит,
sin( +
+  ) = sin
) = sin cos
cos + cos
+ cos sin
sin .
.
sin( -
-  ) = sin(
) = sin( + (-
+ (- )) = sin
)) = sin cos(-
cos(- ) + cos
) + cos sin(-
sin(- ) = sin
) = sin cos
cos - cos
- cos sin
sin .
.
Значит,
sin( -
-  ) = sin
) = sin cos
cos - cos
- cos sin
sin .
.
№ 17
Формулы двойных углов
Формулы сложения позволяют выразить sin 2![]() , cos 2
, cos 2![]() , tg 2
, tg 2![]() , ctg 2
, ctg 2![]() через тригонометрические функции угла
через тригонометрические функции угла ![]() .
.
Положим в формулах
sin(![]() +
+ ![]() ) = sin
) = sin![]() cos
cos![]() + cos
+ cos![]() sin
sin![]() ,
,
cos(![]() +
+ ![]() ) = cos
) = cos![]() cos
cos![]() - sin
- sin![]() sin
sin![]() ,
,
![]() ,
,
![]() .
.
![]() равным
равным ![]() . Получим тождества:
. Получим тождества:
sin 2![]() = 2 sin
= 2 sin ![]() cos
cos ![]() ;
;
cos 2![]() = cos2
= cos2 ![]() - sin2
- sin2 ![]() = 1 - sin2
= 1 - sin2 ![]() = 2 cos2
= 2 cos2 ![]() - 1;
- 1;
![]() ;
; ![]() .
.
№ 18
Формулы половинного аргумента
- Выразив правую часть формулы cos 2
 = cos2
= cos2  - sin2
- sin2  через одну тригонометрическую функцию (синус или косинус), придем к соотношениям
через одну тригонометрическую функцию (синус или косинус), придем к соотношениям
cos 2 = 1 - sin2
= 1 - sin2  , cos 2
, cos 2 = 2 cos2
= 2 cos2  - 1.
- 1.
Если в данных соотношениях положить =
=  /2, то получим:
/2, то получим:
cos = 1 - 2 sin2
= 1 - 2 sin2  /2, cos 2
/2, cos 2 = 2 cos2
= 2 cos2  /2 - 1. (1)
/2 - 1. (1) - Из формул (1) следует, что
 (2),
(2),  (3).
(3). - Разделив почленно равенство (2) на равенство (3), получим
 (4).
(4). - В формулах (2), (3) и (4) знак перед радикалом зависит от того, в какой координатной четверти находится угол
 /2.
/2. - Полезно знать следующую формулу:
 .
.
№ 19
Формулы суммы и разности синусов, косинусов
Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций. Формулы, на которых основано такое преобразование, могут быть получены из формул сложения.
Чтобы представить в виде произведения сумму sin ![]() + sin
+ sin ![]() , положим
, положим ![]() = x + y и
= x + y и ![]() = x - y и воспользуемся формулами синуса суммы и синуса разности. Получим:
= x - y и воспользуемся формулами синуса суммы и синуса разности. Получим:
sin ![]() + sin
+ sin ![]() = sin (x + y) + sin (x - y) = sinx cosy + cosx siny + sinx cosy - cosx siny = 2sinx cosy.
= sin (x + y) + sin (x - y) = sinx cosy + cosx siny + sinx cosy - cosx siny = 2sinx cosy.
Решив теперь систему уравнений ![]() = x + y,
= x + y, ![]() = x - y относительно x и y, получим х =
= x - y относительно x и y, получим х = ![]() , y =
, y = ![]() .
.
Следовательно,
sin ![]() + sin
+ sin ![]() = 2 sin
= 2 sin![]() cos
cos![]() .
.
Аналогичным образом выводят формулы:
sin ![]() -sin
-sin ![]() = 2 cos
= 2 cos![]() sin
sin ![]() ;
;
cos ![]() + cos
+ cos ![]() = 2 cos
= 2 cos![]() cos
cos![]() ;
;
cos ![]() + cos
+ cos