Контрольная работа: Алгебра матриц. Системы линейных уравнений

Алгебраические дополнения:

Транспонированная матрица алгебраических дополнений (союзная матрица):

Запишем выражение для обратной матрицы:

Вычислим столбец неизвестных:

Тема: Решение систем линейных уравнений методом Крамера и Гаусса

Задание 1: Исследовать и решить систему по формулам Крамера:

Найти решение системы уравнений по методу Крамера.

Согласно методу Крамера, если определитель матрицы системы ненулевой, то система из 4-х уравнении имеет одно решение, при этом значение корней:

,,,,

Где:

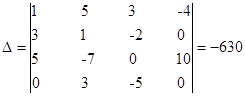- определитель матрицы коэффициентов – ненулевой.

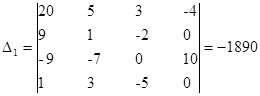- определитель матрицы полученной путем замены первого столбца матрицы коэффициентов на столбец свободных членов.

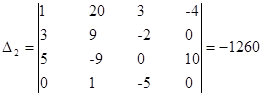- определитель матрицы полученной заменой второго столбца матрицы коэффициентов на столбец свободных членов.

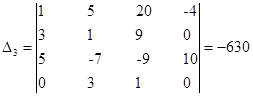- определитель матрицы полученной заменой третьего столбца матрицы коэффициентов на столбец свободных членов.

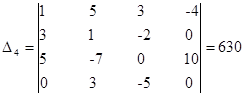- определитель матрицы полученной заменой четвертого столбца матрицы коэффициентов на столбец свободных членов.

Итак:

,

,

.

Задание 2: Решить эту систему по методу Гаусса.