Контрольная работа: Анализ поведения функций при заданных значениях аргумента
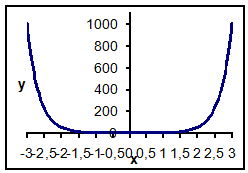
Гиперболические: функция 
1. Область существования:
2. Четность:
функция четная
3. Функция непрерывна
4. Точки пересечения функции с осями координат: (0, 0)
5. Экстремум функции
Значения функции
| x | y | x | y | x | y |
| -3 | 1010,369 | -1 | 2,131145 | 1 | 2,131145 |
| -2,9 | 748,0854 | -0,9 | 1,510096 | 1,1 | 2,976561 |
| -2,8 | 553,8202 | -0,8 | 1,054878 | 1,2 | 4,125531 |
| -2,7 | 409,9402 | -0,7 | 0,722286 | 1,3 | 5,685108 |
| -2,6 | 303,383 | -0,6 | 0,480502 | 1,4 | 7,799941 |
| -2,5 | 224,4723 | -0,5 | 0,306196 | 1,5 | 10,66543 |
| -2,4 | 166,0397 | -0,4 | 0,182396 | 1,6 | 14,54546 |
| -2,3 | 122,7752 | -0,3 | 0,096937 | 1,7 | 19,79642 |
| -2,2 | 90,74509 | -0,2 | 0,04135 | 1,8 | 26,8995 |
| -2,1 | 67,03564 | -0,1 | 0,010084 | 1,9 | 36,50441 |
| -2 | 49,48836 | 0 | 0 | 2 | 49,48836 |
| -1,9 | 36,50441 | 0,1 | 0,010084 | 2,1 | 67,03564 |
| -1,8 | 26,8995 | 0,2 | 0,04135 | 2,2 | 90,74509 |
| -1,7 | 19,79642 | 0,3 | 0,096937 | 2,3 | 122,7752 |
| -1,6 | 14,54546 | 0,4 | 0,182396 | 2,4 | 166,0397 |
| -1,5 | 10,66543 | 0,5 | 0,306196 | 2,5 | 224,4723 |
| -1,4 | 7,799941 | 0,6 | 0,480502 | 2,6 | 303,383 |
| -1,3 | 5,685108 | 0,7 | 0,722286 | 2,7 | 409,9402 |
| -1,2 | 4,125531 | 0,8 | 1,054878 | 2,8 | 553,8202 |
| -1,1 | 2,976561 | 0,9 | 1,510096 | 2,9 | 748,0854 |
| -1 | 2,131145 | 1 | 2,131145 | 3 | 1010,369 |
График функции
 |
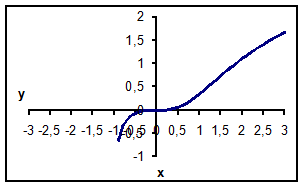
Натуральные логарифмы:функция
1. Область существования:
2. Четность:
функция ни четная, ни нечетная
3. Функция непрерывна.4. Точки пересечения функции с осями координат: (0, 0)
5. Экстремум функции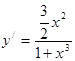
6. Точки перегиба:
, 
Значения функции
| x | y | x | y |
| -1 | 1 | 0,346574 | |
| -0,9 | -0,65282 | 1,1 | 0,423149 |
| -0,8 | -0,35872 | 1,2 | 0,501784 |
| -0,7 | -0,21004 | 1,3 | 0,581106 |
| -0,6 | -0,12167 | 1,4 | 0,660077 |
| -0,5 | -0,06677 | 1,5 | 0,737953 |
| -0,4 | -0,03307 | 1,6 | 0,814228 |
| -0,3 | -0,01369 | 1,7 | 0,888577 |
| -0,2 | -0,00402 | 1,8 | 0,960809 |
| -0,1 | -0,0005 | 1,9 | 1,03083 |
| 0 | 0 | 2 | 1,098612 |
| 0,1 | 0,0005 | 2,1 | 1,164175 |
| 0,2 | 0,003984 | 2,2 | 1,227567 |
| 0,3 | 0,013321 | 2,3 | 1,288857 |
| 0,4 | 0,031018 | 2,4 | 1,348124 |
| 0,5 | 0,058892 | 2,5 | 1,405454 |
| 0,6 | 0,097783 | 2,6 | 1,460935 |
| 0,7 | 0,147453 | 2,7 | 1,514656 |
| 0,8 | 0,206717 | 2,8 | 1,566703 |
| 0,9 | 0,273772 | 2,9 | 1,617158 |
| 1 | 0,346574 | 3 | 1,666102 |
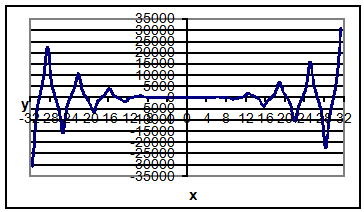
Сочетание тригонометрических, гиперболических:функция 
1. Область существования:
.Точка разрыва.
2. Четность:
функция четная.
4. Точек пересечения функции с осями координат нет.
5. Экстремум функции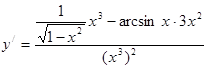
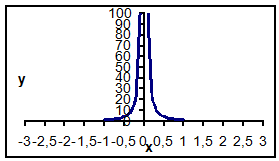
Значения функции
| x | y |
| -1 | 1,570796 |
| -0,9 | 1,536035 |
| -0,8 | 1,811123 |
| -0,7 | 2,260634 |
| -0,6 | 2,979172 |
| -0,5 | 4,18879 |
| -0,4 | 6,429951 |
| -0,3 | 11,28491 |
| -0,2 | 25,16974 |
| -0,1 | 100,1674 |
| 0 | |
| 0,1 | 100,1674 |
| 0,2 | 25,16974 |
| 0,3 | 11,28491 |
| 0,4 | 6,429951 |
| 0,5 | 4,18879 |
| 0,6 | 2,979172 |
| 0,7 | 2,260634 |
| 0,8 | 1,811123 |
| 0,9 | 1,536035 |
| 1 | 1,570796 |
Задание 2. Выполнить исследование методами математического анализа уравнения функции и определить значения аргумента и параметра (если он имеется). Вид уравнения выбирается самостоятельно
Циссоида
(
Обе функции 
и 
определены при всех значениях 
. Заметим, что , 
при 
. Найдем производные 
и 
:
при,
при .