Контрольная работа: Асинхронные двигатели

Обмотка ротора, как и обмотка статора, является многофазной и при появлении в ней тока создаёт своё вращающееся магнитное поле. Обозначим через n2 частоту вращения магнитного поля ротора относительно ротора.

n2 = (60 f2) / p= (60 f S) / p.

Здесь p – число пар полюсов обмотки ротора, оно всегда равно числу пар полюсов обмотки статора.

Относительно статора магнитное поле ротора вращается с частотой

Из полученного соотношения следует, что магнитное поле ротора относительно статора вращается с той же частотой, что и магнитное поле статора. Таким образом, магнитные поля ротора и статора относительно друг друга неподвижны. Поэтому при анализе работы асинхронной машины можно применить те же соотношения, что и трансформаторе.

Ток статора

Так как результирующее магнитное поле асинхронной машины не зависит от её режима работы, можно составить для одной фазы уравнение магнитодвижущих сил, приравняв магнитодвижущую силу в режиме холостого хода к сумме магнитодвижущих сил в режиме нагрузки.

– составляющая тока статора, которая компенсирует действие магнитодвижущей силы обмотки ротора. Полученное выражение для тока статора отражает свойство саморегулирования асинхронной машины. Чем больше ток ротора, тем больше ток статора. В режиме холостого хода ток статора минимальный. В режиме нагрузки ток статора возрастает. Ток реального холостого хода асинхронной машины и значительно больше по сравнению с номинальным током, чем у трансформатора. Это объясняется тем, что величина тока I0 зависит от магнитного сопротивления среды, в которой создаётся магнитное поле. У асинхронной машины, в отличие от трансформатора, есть воздушный зазор, который создаст большое сопротивление магнитному полю.

Электромагнитный момент асинхронной машины

Электромагнитный момент возникает при наличии магнитного поля, создаваемого обмоткой статора, и тока в обмотке ротора. Можно показать, что электромагнитный момент определяется соотношением:

М=СФI2cosψ2.

Здесь: – конструктивный коэффициент;

ω0 = 2 π f / p – скорость вращения магнитного поля;

ψ2 – сдвиг по фазе между ЭДС и током ротора;

I2 cos ψ2 – активная составляющая тока ротора.

Таким образом, величина электромагнитного момента зависит от результирующего магнитного поля Ф и активной составляющей тока ротора.

На рис. 2.12 приведено пояснение влияния cosψ2 на величину электромагнитного момента: а) ψ2 = 0°, (cos ψ2 = 1); б) ψ2 = 90°, (cos ψ2 = 0).

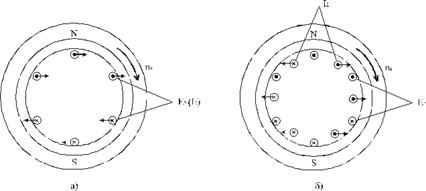
Рис. 2.12.

Как следует из рис. 2.12а, если ψ2 = 0°, в создании электромагнитного момента участвуют все проводники обмотки ротора, т.е. момент имеет наибольшее значение. Если ψ2 = 90° (рис. 2.12 б), результирующая электромагнитная сила и момент равны нулю.

В режиме двигателя при изменении нагрузки на валу изменяется частота вращения ротора, что приводит к изменению скольжения, частоты тока ротора, индуктивного сопротивления ротора и cosψ2. В результате изменяется вращающий момент. На рис. 2.13 приведено пояснение влияния индуктивного сопротивления ротора на угол ψ2: а) при S=1 (пуск в ход); при S≤1 (после разгона). Наибольшие значения ЭДС и частота тока ротора имеют в момент пуска в ход, когда скольжение S=1. При этом f2 = f1, X2 >> R2, угол ψ2 близок к 90° (рис. 2.13 а).

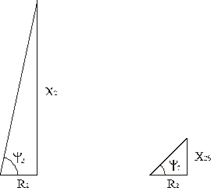
Рис. 2.13

За счет малого cosψ2 в момент пуска в ход асинхронные двигатели имеют ограниченный пусковой момент. Кратность пускового момента (по сравнению с номинальным) у них составляет

Мпуск / Mн = 0,8 ÷ 1,8.

Причем большие цифры относятся к двигателям специальной конструкции с улучшенными пусковыми свойствами.

По мере разгона ротора двигателя частота тока ротора падает, уменьшается индуктивное сопротивление ротора Х2S и угол ψ2 уменьшается (рис. 2.13 б). Это приводит к увеличению вращающего момента и дальнейшему разгону двигателя.

Подставим в выражение для электромагнитного момента соотношения для I2, cosψ2 и Ф, полученные ранее: