Контрольная работа: Частотные характеристики дискретных систем управления

???. 1

Пусть на вход системы подается сигнал или в комплексной форме , при этом сигнал на выходе импульсного элемента равен или в комплексной форме , где представляет собой безразмерную частоту.

Для непрерывной системы зависимость между входным и выходным сигналом определяется через интеграл свертки

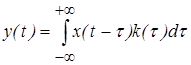. (1)

Для дискретных систем это соотношение имеет вид:

(2)

где 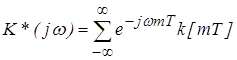- комплексный коэффициент передачи.

Для построения частотных характеристик используется соотношение

. (3)

Это выражение представляет собой сумму векторов до точек и т. д., при этом количество необходимых векторов зависит от ширины полосы пропускания системы. Если частота квантования велика по сравнению с шириной полосы пропускания, то достаточно использовать 2-3 члена суммы ряда.

Выражения для амплитудно-частотной и фазочастотной характеристик определяются из соотношений

, (4)

.

Так как частотные характеристики являются периодическими функциями частоты с периодом 2p, то они полностью определяются ее значениями на интервале . Так как АФХ дискретной системы является симметричной относительно действительной оси (в соответствии со свойством дискретного преобразования Фурье), то ее достаточно рассматривать на интервале частот .

Пример 1. Построить АФХ дискретной системы, если передаточная функция ее непрерывной части имеет вид

.

Решение: Передаточная функция дискретной системы имеет вид

, где .

Выполнив подстановку р = jw, получим

.

Изменяя частоту на интервале , находим соответствующие значения K*(jw), которые заносим в таблицу 1.

Таблица 1

w	0	p/2T	p/T
K*(jw)			« 1 2 3 4 » К-во Просмотров: 226 Бесплатно скачать Контрольная работа: Частотные характеристики дискретных систем управления >>> Скачать <<< Меню Поиск