Контрольная работа: Дифференцирование. Интегрирование

Функция возрастает в промежутке (-∞; – 1) U (1; ∞)

и убывает в промежутке (-1; 0) U (0; 1).

Функция имеет экстремумы : максимум – в точке х=-1, минимум – в точке х=1.

Исследуем функцию на выпуклость / вогнутость .

Для этого найдем производную второго порядка и, приравняв её к нулю, вычислим критические точки второго рода.

В точке х=0 вторая производная не существует, т. к. это точка разрыва функции. В интервале (-∞; 0) <0, следовательно, график функции в этом интервале выпуклый. В интервале (0;∞) >0, следовательно, график функции в этом интервале вогнутый.

Асимптоты графика функции :

1) вертикальная асимптота – прямая х=0

Т.к. и

2) горизонтальных асимптот нет,

т. к. и

3) наклонных асимптот нет,

т. к.

и

Задание 3 . Найти экстремумы функции Z = ln (3 – x ² + 2 x – y ² )

Найдем частные производные первого порядка.

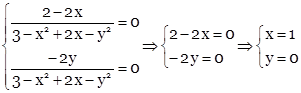
М (1; 0) – стационарная точка.

Найдем вторые производные и их значения в точке М.

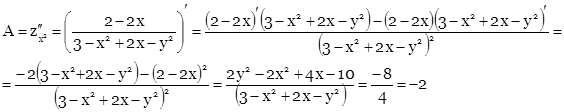
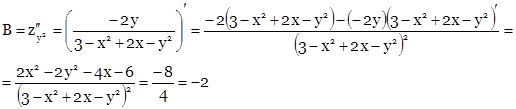
>0 Следовательно, функция Z = ln (3 – x ² + 2 x – y ² ) имеет экстремум в точке М (1; 0) – максимум, т. к. A < 0.

Задание 4 . Вычислить неопределенные интегралы, результат проверить дифференцированием

a)