4) в появившемся диалоговом окне «Анализ данных» (рис. 5) выбрать «Регрессия»;

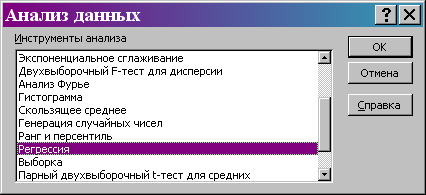
Рис. 5. Диалоговое окно «Анализ данных».

5) в появившемся диалоговом окне «Регрессия» (рис. 6) убедиться, что все проставленные в нем установки соответствуют таблице исходных данных. После выполнения этих операций нажать клавишу «ОК»;

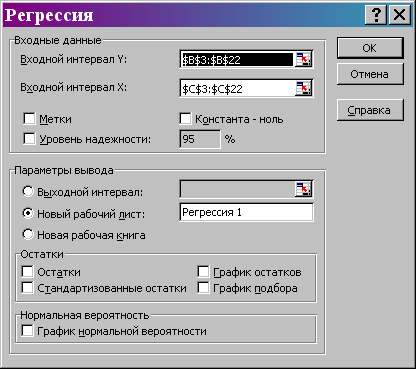
Рис. 6. Диалоговое окно «Регрессия».

В результате получим:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,416713
R-квадрат	0,17365
Нормированный R-квадрат	0,09368
Стандартная ошибка	7,58219
Наблюдения	35
Дисперсионный анализ
df	SS	MS	F	Значимость F
Регрессия	3	374,508	124,836	2,171453	0,111346483
Остаток	31	1782,178	57,4896
Итого	34	2156,686
Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	56,84826	10,01268	5,677626	3,08E-06	36,42724917	77,26927	36,42725	77,26927
Х1	0,440965	0,306967	1,436523	0,16087	-0,185098139	1,067027	-0,1851	1,067027
Х2	-0,11314	0,13485	-0,83899	0,407899	-0,388166847	0,161891	-0,38817	0,161891
Х3	0,104629	0,058561	1,786669	0,083775	-0,014806871	0,224065	-0,01481	0,224065

Уравнение регрессии полученное с помощью Excel, имеет вид:

3. По данным проведенного корреляционного и регрессионного анализа оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

Общий F-критерий проверяет гипотезу о статистической значимости уравнения регрессии. Анализ выполняется при сравнении фактического и табличного значения F-критерия Фишера.

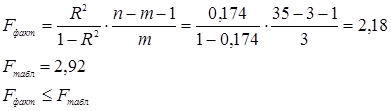
Частные F-критерии оценивают статистическую значимость присутствия факторов в уравнении регрессии, оценивают целесообразность включения в уравнение одного фактора после другого.

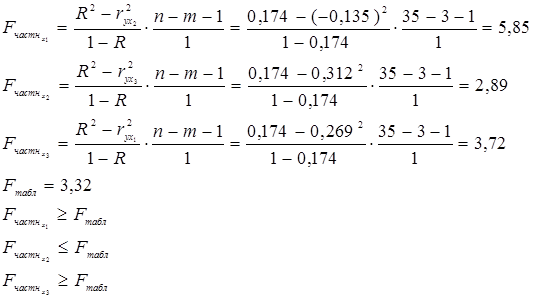
t-критерий проверяет гипотезу о статистической значимости факторов уравнения регрессии.

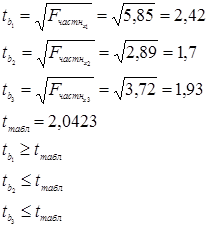
4. Согласно проведенному анализу информативными факторами являются х₁ и х₂ , а также коэффициенты b₁ и b_2. Следовательно уравнение регрессии со статистически значимыми факторами будет иметь вид:

5. Аналитическая записка.

По результатам проведенного корреляционного анализа можно сказать, что межфакторная связь слабая, т.к. значения коэффициентов парной корреляции не превышают значения 0,4, хотя можно сказать, что наибольшая связь результативного признака с и .

Мультиколлинеарность отсутствует, т.к. ни одно значение коэффициентов не превышает 0,7.

Фактическое значение F-критерия Фишера меньше табличного, следовательно можно сказать, что полученное уравнение регрессии статистически незначимо.

По полученным значениям частных F-критериев Фишера, можно сказать, что включение фактора х₂ после х₃ оказался статистически незначимым: прирост факторной дисперсии (в расчете на одну степень свободы) оказался несущественным. Следовательно, регрессионная модель зависимости бонитировочного балла от количества минеральных удобрений, внесенных в почву и запасов влаги в почве является достаточно статистически значимой и что нет необходимости улучшать ее, включая дополнительный фактор х₂ (коэффициент износа основных средств).

Это предположение подтверждает оценка с помощью t-критерия Стьюдента значимости коэффициентов. По результатам этой оценки:

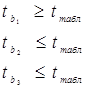
т.е. можно сказать, что b₂ и b₃ статистически незначимы.

В совокупности с результатами F-статистики, делаем вывод, что из уравнения регрессии можно исключить х₂ и b₂ .

ЗАДАЧА 3.

В таблице приведены данные по природно-экономической зоне за 15 лет об урожайности многолетних трав на сено У, внесении удобрений на 1 га пашни Х1 и осадках за май-июнь месяцы Х2.

номер года	у	х1	х2
1	13,6	161	360
2	14,1	170	223
3	13,2	188	144
4	18,6	209	324
5	16,9	240	227
6	21	334	212
7	22,2	377	230
8	29,6	399	204
9	31,3	404	156
10	32,1	451	200
11	26,7	501	163
12	32,8	538	315
13	31,4	579	280
14	31	600	251
15	26,1	614	386

Задание следует выполнить с помощью ППП MSEXCEL или любого статистического пакета прикладных программ.

Задание.

Необходимо проанализировать степень зависимости урожайности У от факторов Х1 и Х2, для этого:

1. Определить для каждого ряда данных У, Х1, Х2 первые разности (абсолютные приросты).

2. Рассчитать параметры двухфакторного линейного уравнения регрессии по первым разностям (по абсолютным приростам) и дать их интерпретацию. Охарактеризовать тесноту связи между рядами.

3. Оценить полученные результаты, выводы оформить в виде аналитической записки.

Решение.

1. Значения абсолютных приростов определяются по формулам:

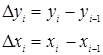
Расчеты можно оформить в виде таблицы:

Номер года
1
2	0,5	9	-137
3	-0,9	18	-79
4	5,4	21	180
5	-1,7	31	-97
6	4,1	94	-15
7	1,2	43	18
8	7,4	22	-26
9	1,7	5	-48
10	0,8	47	44
11	-5,4	50	-37
12	6,1	37	152
13	-1,4	41	-35
14	-0,4	21	-29
15	-4,9	14	135

2. Для проведения корреляционного анализа воспользуемся программой «Excel»:

1) загрузить среду Excel ;

2) выделить рабочее поле таблицы;