Контрольная работа: Электрофизические процессы в электрических аппаратах
Эту механическую силу называют электродинамической. Электродинамические силы возникают не только в контуре с током, расположенным во внешнем магнитном поле, но и в случае, когда этот контур уединен, и поле, его окружающее, определяется током в самом контуре.
При прохождении тока к. з., превышающего номинальный в 10–20 раз, на токоведущей контур электрического аппарата воздействуют значительные электродинамические силы, стремящиеся деформировать этот контур. При прохождении тока по соседним токоведущим контурам также возникают силы, которыми контуры взаимодействуют между собой. В сильноточных электрических аппаратах электродинамические силы могут достигать десятков тысяч ньютон. Способность электрического аппарата противостоять механическим нагрузкам, возникающих в токоведущих частях и поддерживающих их элементах в режиме к. з., называется электродинамической стойкостью.
Электродинамические силызависят от наибольшего значения тока, от длины, конфигурации и взаимного расположения деталей, образующих токоведущий контур, а также от магнитных свойств окружающей среды. Токоведущие части могут располагаться как в среде с постоянной магнитной проницаемостью, не зависящей от напряженности магнитного поля (воздух, жидкие твердые изоляционные материалы), так и в среде, магнитная проницаемость которой зависит от напряженности магнитного поля.
Электродинамические силы определяются или с помощью закона Ампера (формула 3), или по изменению запаса магнитной энергии токоведущего контура. Первый метод рекомендуется применять тогда, когда можно аналитически найти индукцию в любой точке проводника, для которого необходимо определить силу. Индукцию определяют, используя закон Био-Савара-Лапласа, согласно которого элементарная индукция dB от элемента dl 2 проводника l 2 с током i 2 в произвольной точке М, в нашем случае принадлежащей элементу dl 1 проводника l 1 , равна (рис. 1):
![]()
 , (2)
, (2)
где ![]() -магнитная проницаемость вакуума равная 4p 10-7 Гн/м; a-угол между током i 2 и лучом r.
-магнитная проницаемость вакуума равная 4p 10-7 Гн/м; a-угол между током i 2 и лучом r.
Индукция в точке М, создаваемая током, проходящим по всему проводнику l 2 :
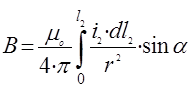 (3)
(3)
Силу, действующую на весь проводник l1 , определим, подставив (3) в (1)
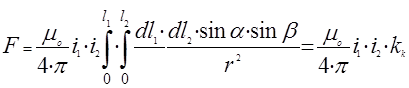 , (4)
, (4)
где kk – коэффициент контура, величина интеграла, зависящая только от геометрических размеров проводников и их взаимного расположения.
Полученные формулы справедливы, когда можно считать, что токи протекают по осям проводников, а форма и размеры сечений проводников не влияют на электродинамические силы.
По формуле (4) определяется суммарная величина электродинамической силы взаимодействия данных проводников или контуров с токами, т.е. равнодействующая электродинамические сил. Точки приложения этой силы зависят от характера распределения электродинамические сил по длине проводников, обусловленного их конфигурацией и взаимным расположением.
Как уже сказано, при втором методе электродинамические силы определяются по изменению запаса магнитной энергии токоведущего контура. Электромагнитное поле вокруг проводников и контуров с током обладает определенным запасом энергии. Электромагнитная энергия контура с током i .
![]() (5)
(5)
Электромагнитная энергия двух контуров, обтекаемых токами i 1 и i 2
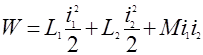 , (6)
, (6)
где L 1 и L 2 - индуктивность контуров; М – взаимная индуктивность контуров.
Всякая деформация контура (изменение расположения его элементов или частей) или изменение взаиморасположения контуров приводят к изменению запаса электромагнитной энергии. При этом работа сил в любой системе равна изменению запаса энергии этой системы:
![]() , (7)
, (7)
здесь dW - изменение запаса энергии системы при деформации системы в направлении х под действием силы F .
На указанном законе и основан второй метод определения электродинамических сил в контурах. Электродинамическая сила в контуре иле между контурами, действующая в направлении х , равна скорости изменения запаса энергии системы при деформации ее в том же направлении:
![]() (8)
(8)
Согласно сказанному электродинамическая сила в контуре, обтекаемом током i
![]() , (9)
, (9)
а электродинамическая сила между двумя взаимосвязанными контурами с токами i 1 и i 2
 (10)
(10)
Рассмотрим электродинамические силы в наиболее простых случаях взаимного расположения проводников как при допущении, что форма и размеры сечений проводников не влияют на электродинамические силы, а токи протекают по осям проводников, так и с учетом формы и размеров сечений.
Направление вектора силы Ампера ![]() определяется по правилу левой руки: вектор магнитной индукции
определяется по правилу левой руки: вектор магнитной индукции ![]() входит в ладонь, четыре пальца направлены вдоль тока, большой отогнутый палец покажет направление вектора силы. При этом направление вектора магнитной индукции определяется следующим образом. Если смотреть вдоль проводника по направлению тока, то вектор магнитной индукции направлен по ходу часовой стрелки.
входит в ладонь, четыре пальца направлены вдоль тока, большой отогнутый палец покажет направление вектора силы. При этом направление вектора магнитной индукции определяется следующим образом. Если смотреть вдоль проводника по направлению тока, то вектор магнитной индукции направлен по ходу часовой стрелки.
Модуль электродинамические силы определяются или с помощью закона Ампера, или по изменению запаса магнитной энергии токоведущего контура.
1. Электродинамические силы между параллельными проводниками бесконечной длины
Если токи в параллельных проводниках направлены одинаково, то векторы силы направлены навстречу друг другу – проводники испытывают взаимное притяжение. Если токи в параллельных проводниках направлены противоположно, то наоборот – проводники отталкиваются.
И для искомой электродинамической силы, действующей на участок l1 проводника с током i1 можно записать