Контрольная работа: Электрофизические процессы в электрических аппаратах

где – расстояние между проводниками.

Электродинамические силы между проводниками, расположенными под прямым углом.

Если l₂ ®¥, то полная сила, действующая на проводник конечной длины l₁ -r

, (12)

где r – радиус круглого проводника.

Если l₂ конечная длина, то полная сила, действующая на проводник конечной длины l₁ -r

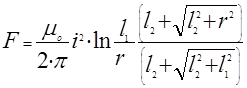(13)

Рассмотренные случаи взаимного расположения проводников параллельно друг другу и под прямым углом имеют широкое распространение в электрических аппаратах.

2. Электродинамические силы в круговом витке

В круговом витке с током i возникают радиальные силы f стремящиеся увеличить его периметр, т.е. разорвать виток. Электродинамическая сила, действующая на весь виток, рассчитывается по формуле:

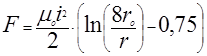(14)

Электродинамическая сила F_x , стремящаяся разорвать виток, определяется как сумма горизонтальных составляющих сил f на четверти длины окружности:

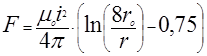(15)

3. Электродинамические силы в месте изменения сечения проводника

При изменении поперечного сечения проводника происходит искривление линий тока. Так как сила dF нормальна к линиям тока, то она наклонена в сторону большего сечения. Эту силу можно разложить на две составляющие: поперечную сжимающую dF_{c ж} и продольную dF_пр . Продольная составляющая, называемая электродинамической силой сужения, стремится разорвать проводник в месте изменения сечения и направлена от меньшего сечения к большему.

Для проводника круглого сечения полная сила, действующая по оси проводника

(16)

Для некруглого сечения выражение (26) приобретает вид

, (17)

где S₁ и S₂ – большое и малое поперечное сечение проводника.

Из формул (16) и (17) следует, что продольная электродинамическая сила сужения зависит от соотношения величин большого и малого сечений проводника и не зависит от длины и формы перехода от одного сечения к другому, а также от направления тока.

4. Электродинамические силы при наличие в контуре ферромагнитных деталей

Так как магнитный поток проводника с током стремится замкнуться по ферромагнитной детали, имеющей малое магнитное сопротивление, то магнитное поле между проводником с током и ферромагнитной деталью ослаблено, а сила всегда направлена в сторону ослабленного магнитного поля. Определить эту силу можно, если заменить воздействие ферромагнитной детали симметрично расположенным таким же проводником (применить его зеркальное изображение). Следовательно, электродинамическую силу взаимодействия между проводником с током и ферромагнитной деталью можно определить как силу взаимодействия между двумя параллельными проводниками, расположенными под некоторым углом, если ферромагнитная деталь расположена под этим углом к проводнику, с одинаковыми токами одного направления. Таким образом, в общем виде сила взаимодействия и фактическое ее значение определяется в каждом случае соответствующим значением k_k .

Электродинамические силы при переменном токе

Приведенные выше уравнения справедливы и для переменного тока, но в этом случае сила будет изменяться во времени (но не в пространстве) по определенному закону. Для расчетов аппаратов на электродинамическую стойкость важно знать максимальное значение этой силы.

Рассмотрим однофазную систему переменного тока . Ток изменяется по закону , где I_т – амплитудное значение. Тогда, учитывая, что sin² wt=(1-cos2wt)/2, мгновенное значение электродинамической силы между отдельными частями проводника

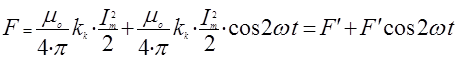(18)

Из формулы (18) следует, что в однофазной цепи электродинамическая сила состоит из двух составляющих (рис. 7.): постоянной, не изменяющейся во времени