1. Прибор может работать в двух режимах ¾ нормальном и ненормальном. Нормальный режим встречается в 80% всех случаев работы прибора, ненормальный ¾ в 20%. Вероятность выхода прибора за время t в нормальном режиме равна 0,1, в ненормальном ¾ 0,7. Найти вероятность выхода прибора из строя за время t .

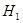
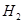Решение

Пусть гипотезы и состоят в том что прибор работает:

- в нормальном режиме, вероятность

- в ненормальном режиме, вероятность

Гипотезы несовместны и сумма их вероятностей равна 1. Значит, гипотезы образуют полную группу.

Пусть событие А состоит в том, что прибор выходит из строя. При условии, что режим работы нормальный, вероятность наступления А равна

При условии что режим работы ненормальный вероятность наступления А

?? ??????? ?????? ??????????? ???????? ??????????? ???? ??? ?????? ?????? ?? ????? ?? ????? t

Ответ: 0,22

2. В лотерее каждый десятый билет выигрывает 10 рублей, сам же лотерейный билет стоит 1 рубль. Некто приобрел 10 билетов. Найти вероятность того, что он:

а) не будет в проигрыше;

б) будет в выигрыше.

Решение

Вероятность выиграть по произвольному билету, по формуле классической вероятности равна p=0.1

Проводится n=10 испытаний c одинаковой вероятностью наступления события в каждом.

Для того чтобы игрок не был в проигрыше, должен выиграть хотя бы один билет то есть k>=1

Для того чтобы игрок был в выигрыше, должно выиграть как минимум два билета или k>1

По формуле Бернулли,

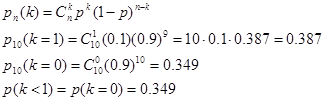
Теперь найдем вероятность противоположного события p(k>=1)=1-p(k<1)=1-0.349=0.651 – вероятность не оказаться в проигрыше

P(k>=1)=p(k>1)+p(k=1) – вероятность суммы несовместных событий

P(k>1)=p(k>=1)-p(k=1)=0.651-0.387=0.264 – вероятность выигрыша

Ответ: а)0,651 б)0,264

3. Семена некоторых растений прорастают с вероятностью 0,8. Найти вероятность того, что из 2000 посаженных семян прорастает:

а) 1600 семян;

б) не менее 1600 семян.

Решение

Мы имеем дело с серией последовательных независимых испытаний, в каждом из которых с одинаковой вероятностью может произойти событие А (семя прорастает)

Количество испытаний n=2000

Вероятность наступления события А равна p(A)=0.8=p

--> ЧИТАТЬ ПОЛНОСТЬЮ <--