Закон распределения Пуассона выражается формулой (1.1).

Будем моделировать интервал времени между двумя последовательно зашедшими в банк клиентами методом Монте-Карло с датчиком случайных чисел на интервале [0 - 1].

Совокупность независимых случайных событий, образующих полную группу, характеризуется вероятностями появления каждого из событий , причем . Для моделирования этой совокупности случайных событий используется генератор случайных чисел, равномерно распределенных в интервале [0 - 1]. При делении отрезка [0 - 1] на n частей, численно равных , возникновение события устанавливается путем определения нахождения случайного числа Х в пределах интервала при проверке условия , где изменяется от нуля до n. При имеем ; при имеем и так далее. При подстановке в формулу (1.1) получим:

;

;

и так далее.

Причем (мин.) – максимальное количество ожидания клиентов.

Так как опыт проводится многократно, то, очевидно, что частота попадания случайных чисел на каждый из отрезков, определяющихся их длиной, и соответствует полученным вероятностям

Моделирование времени обслуживания клиентов у касс происходит по экспоненциальному закону распределения, формула которого представлена выше (формула (1.2)).

Время обслуживания клиентов , как и любая иная случайная величина, описывается функцией распределения , определяемая как вероятность случайного события, заключающегося в том, что время обслуживания клиентов меньше некоторого заданного времени :

Эта вероятность рассматривается как функция во всем диапазоне возможных значений величины . Функция распределения любой случайной величины является неубывающей функцией времени . Примерный вид функции дан на рисунке 3.

Рис. 3 – «Функция распределения экспоненциального закона»

Так как значения не могут быть отрицательными, то . При величина стремится к единице. Таким образом, функция распределения времени обслуживания клиентов:

(1.3)

где - параметр распределения (среднее время обслуживания клиентов у кассы).

Соответственно плотность распределения:

(1.4)

Для моделирования времени обслуживания клиента у кассы проинтегрируем функцию распределения :

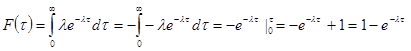
(1.5)

От датчика случайных чисел равномерно распределенных на интервале [0 - 1] получаем очередное число Х, которое подставляем в формулу (1.5) и вычисляем :

(1.6)

Из соотношения (1.6) найдем соответствующее Х, которое будем принимать за случайное число, обозначающее время обслуживания данной кассой.

2. ПРОГРАММНОЕ РЕШЕНИЕ

Программа имитационного моделирования работы кассового зала написана на языке C с помощью среды разработки Borland C++ 3.1.

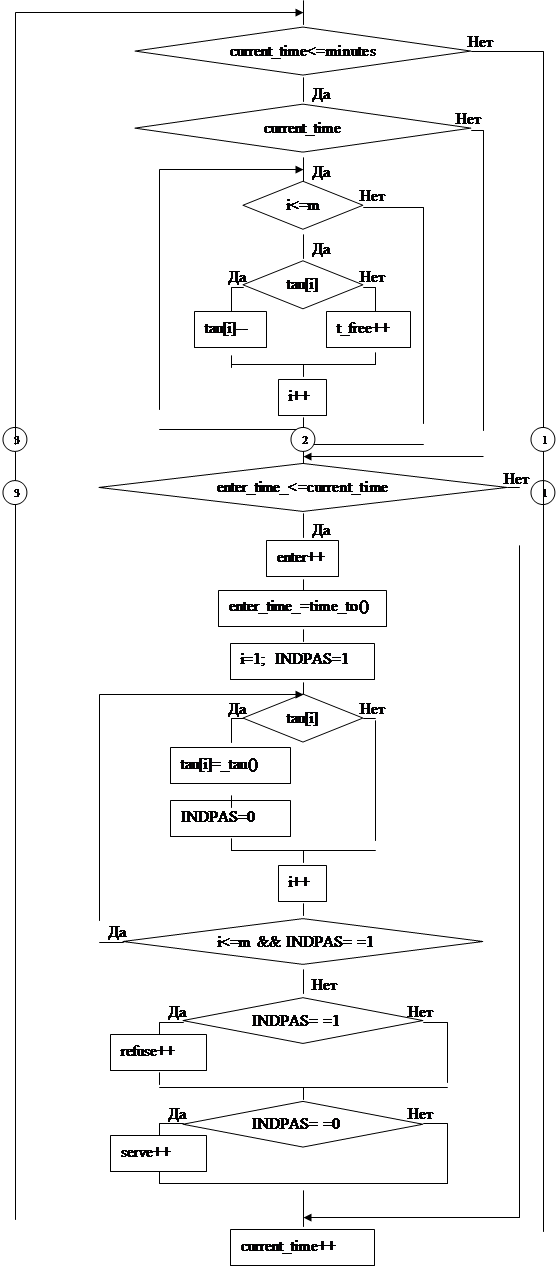
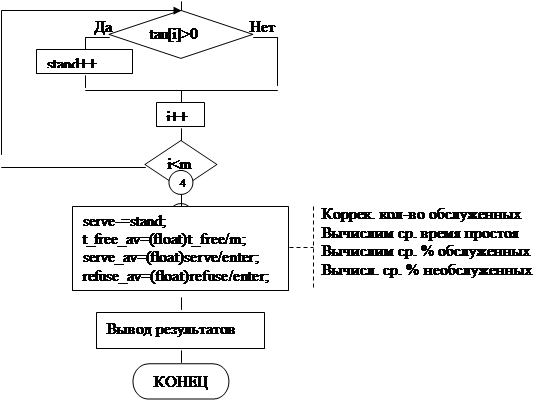
Блок-схема имитационного моделирования работы кассового зала

Исходный текст программы состоит из одного файла Kas1.c который содержит реализацию таких функций программы:

– float RND_DIG (void) - Функция возвращающая СЧ в диапазоне [0, 1];