Контрольная работа: Интегрирование и производная функций

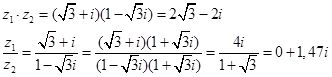
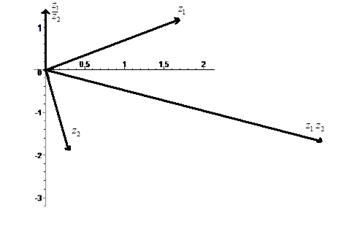
Задание 6

Вычислить производную функции f(z) в точке .

Решение

Так как для аналитических функций справедливы все формулы и правила дифференцирования действительного аргумента, то

Задание 7

Вычислить интеграл по замкнутым контурам а) и б), считая обход контура в положительном направлении. Нарисовать область интегрирования, указать на рисунке особые точки.

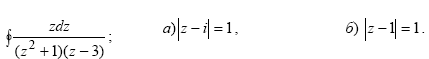
Решение

а)

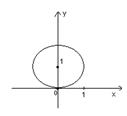
Подынтегральная функция имеет особые точки: . Тогда интеграл вычистится по следующей формуле:

.

б)

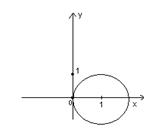
Подынтегральная функция имеет особые точки: . Тогда интеграл вычистится по следующей формуле:

.