Контрольная работа: Исследование системы управления подводного аппарата по вертикальной координате

K2 – коэф. передачи датчика высоты П.А.

К3 – коэф. усиления регулятора.

К4 – коэф. передачи задатчика высоты П.А.

К5 – коэф. скоростной обратной связи.

Схема с введением скоростной обратной связи

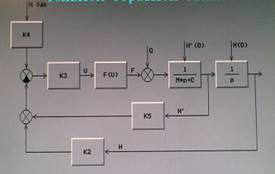
Увеличение К5 не влияет на статическую точность системы, а переходный процесс приближается к апериодическому. При уменьшении К5 переходный процесс становится более колебательным.

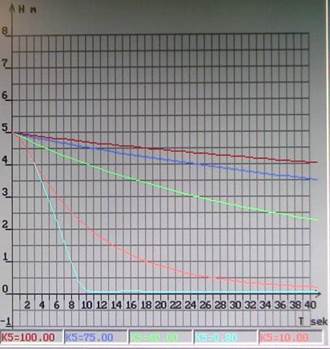
При H=0.1м, К1=400Н/В, К2=1м./В и Q=1000H, К3=25: оптимальное значение коэффициента скоростной обратной связи К5opt=0.8;

Для статической ошибки Нст.=0,5м значение коэффициента К3=Q/K1*K2*Нст.=5;

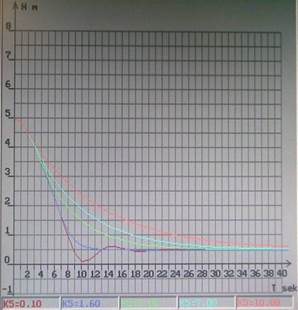
И оптимальное значение К5=1.6;

Выводы: Итак, варьируя значением коэффициента демпфирования К5 можно найти его оптимальное значение, при котором время переходного процесса минимально, а перерегулирование не превышает допустимой величины и не приводит к ударам П.А. о дно. Увеличение К5 по сравнению с его оптимальным значением, затягивает переходный процесс, увеличивая время перехода подводного аппарата на заданную глубину. Уменьшение К5 увеличивает колебательность переходного процесса, перерегулирования при этом могут превысить допустимые пределы и привести к удару аппарата о дно. Изменение К5 не влияет на статическую точность стабилизации высоты подводного аппарата.

4. Изучение релейной схемы управления П.А.

Цель: исследование релейной следящей системы управления П.А. над дном. Для построения такой системы необходимо ввести в состав автоматического регулятора высоты звено с релейной характеристикой. Мы получим нелинейную систему.

Её схема:

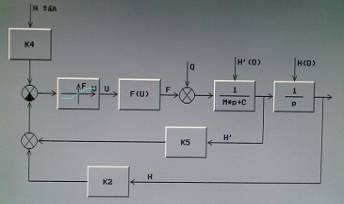
Для исследования используем метод фазовой плоскости, который заключается в построении зависимости скорости движения от его высоты.

Идеальная релейная характеристика

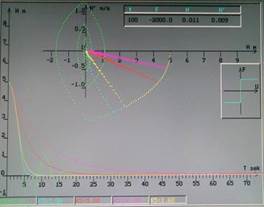
Трёхпозиционное реле

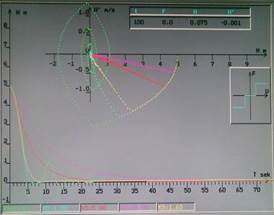
Реле с прямым гистерезисом

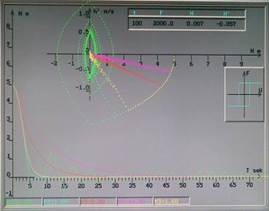
Трёхпозиционное реле с гистерезисом

Линейная характеристика с ограничением

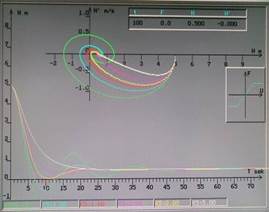
Выводы: Итак, в случае использования реле с идеальной характеристикой, линией переключения является ось ОУ. Система совершает затухающие колебания, асимптотически приближаясь к началу координат – точке устойчивого равновесия.