Контрольная работа: Изучение физического маятника
Амплитуда j0 и фаза aзависят от того, как возбуждаются колебания маятника.
Период колебаний T = 2p/w0 равен:
9) 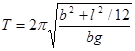 .
.
Период колебаний физического маятника не зависит ни, от фазы, ни от амплитуды колебания. Это утверждение справедливо для колебаний, подчиняющихся уравнение (7). Движение маятника описывается этим уравнением приближенно - в той мере, в какой справедлива использованная при выводе (7) формула sin(j) »j. Исследование правильности утверждения о том, что период колебаний маятника независит от амплитуды, является чувствительным методом проверки теории. Как известно, период колебаний математического маятника определяется формулой:
10) 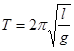 , где l - длина математического маятника.
, где l - длина математического маятника.
Поэтому величина
11) ![]()
называется приведенной длиной физического маятника. Точку О’, отстоящую от точки опоры O на расстояние lпр , называют центром качания физического маятника, Можно доказать, что точка опоры и центр качания маятника обратимы, т.е. при качании маятника вокруг точки O период должен быть таким же, как и при качании вокруг точки O’. Исследование справедливости этого утверждения является другим методам проверки теории. Ещё один метод заключается в проверке правильности формулы (9). Величину b можно изменять, передвигая опорную призму по стержню.
В данной работе в качестве математического маятника используется металлический шарик, подвешенный на двух расходящихся нитях, длину которых можно изменять.
Расчётная часть
После работы с установкой имеем все данные, которые занесены в таблицу и длину физического маятника lизм = 0,6 м.
Теперь построим график зависимости T2 b от b2 .
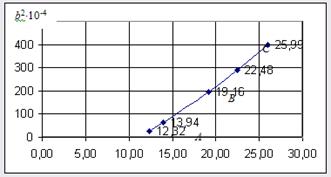
| Физический маятник | |||||
| № | N | b1 ×10-2 м | ti1 , с | ||
| 1 | 40 | 5 | 63,12 | 62,98 | 1,57 |
| 2 | 62,87 | ||||
| 3 | 62,96 | ||||
| № | N | b2 | ti2 , с | ||
| 1 | 40 | 8 | 53,01 | 53 | 1,32 |
| 2 | 52,95 | ||||
| 3 | 53,03 | ||||
| № | N | b3 | ti3 , с | ||
| 1 | 40 | 14 | 46,76 | 46,81 | 1,17 |
| 2 | 46,81 | ||||
| 3 | 46,85 | ||||
| № | N | b4 | ti4 , с | ||
| 1 | 40 | 18 Пересчитывай | 46,06 | 46,01 | 1,15 |
| 2 | 46,01 | ||||
| 3 | 45,95 | ||||
| № | N | b5 | ti5 , с | ||
| 1 | 40 | 20 | 45,54 | 45,64 | 1,14 |
| 2 | 45,78 | ||||
| 3 | 45,61 | ||||
| 2 | 44,97 | ||||
| 3 | 45,07 | ||||
Возьмём несколько точек на графике и найдём по их параметрам (T2 b и b2 ) значения ![]() и
и ![]() для данных точек.
для данных точек.
![]() ;
; ![]() ;
;
Для точки A:
![]() ;
;![]() ;
;
Для точки B:
![]() ;
;![]() ;
;
Для точки С:
![]() ;
;![]() ;
;
По найденным значениям величин ![]() и
и ![]() для точек А, В, С найдём их средние значения:
для точек А, В, С найдём их средние значения:
![]() ;
;![]() ;
;
Отсюда найдём значения g (ускорения свободного падения) и l (реальная длина маятника).
![]() = 10,09 м/с2 . l = 0,57 м.
= 10,09 м/с2 . l = 0,57 м.
Найденное значение l примерно равняется lизм .
Теперь оценим погрешность величины g.
Выражая g из формулы (9) получим формулу вида:  .
.
Вычисление g по данной формуле допускает определение погрешности вычисления величины g по упрощённой формуле.
![]() ;
; ![]() ;
;  ; при DT = Dt имеем:
; при DT = Dt имеем: