Контрольная работа: Компьютерные технологии MS EXEL

- Укажите, где должна находиться новая диаграмма, - На отдельном листе или уже Существующем . Выберите – На существующем листе и нажмите кнопку Готово.

На текущем рабочем листе появится Диаграмма-график . Как и любой объект, его можно выделить и перетащить с помощью мыши на новое место листа (рис.3).

Замечание.

Для построения одного графика Z=F(X) нужно Мастеру диаграмм задать несмежные области листа B2:B22 и D2:D22 , которые можно выделить при нажатой клавише Ctrl .

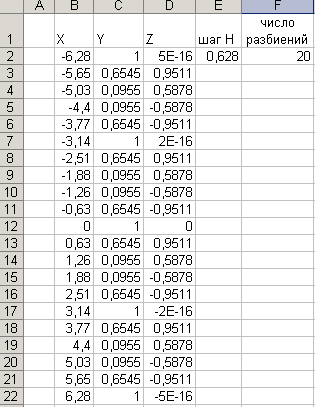
Рис 1.

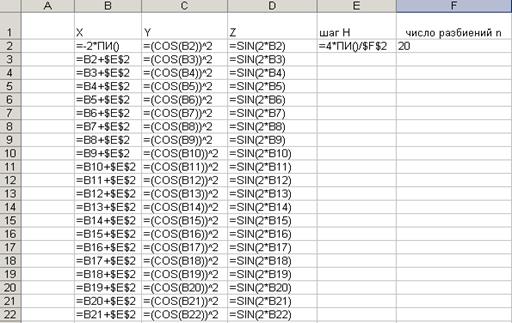
Рис.2

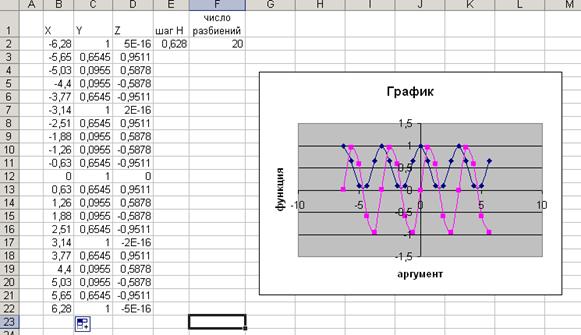
Рис. 3

Варианты заданий

№	Уравнение y=f(x)	Уравнение z=f(x)	Отрезок, содержащий корень	Шаг
1			[2; 3]	0,1
2			[0; 2 ]	0,2
3			[0,4; 1 ]	0,05
4			[0, 0 ,85 ]	0,05
5			[1; 2 ]	0,1
6			[0; 0,8 ]	0,05
7			[ 0 ; 1 ]	0,1
8			[ 2 ; 4 ]	0,2
9			[1; 2 ]	0,1
10			[ 0 ; 2]	0,1
11			[0.1; 1 ]	0,1
12			[ 1 ; 3 ]	0,2
13			[1,2; 2]	0,08
14	ex +lnx-10x=н		[3; 4]	0,1
15			[1; 2]	0,1
16	1-x+sinx-ln(1+x)=y		[0; 1,5]	0,15
17	3x-14+ex -e-x =y		[1; 3]	0,2
18			[0; 1]	0,1
19	x+cos(x0,52 +2)=y		[0,5; 1]	0,05
20	3ln2 x+6lnx-5=y		[1; 3]	0,2
21	sinx2 +cosx2 -10x=y		[0; 1]	0,1
22	x2 – ln(1+x) – 3=y		[2; 3]	0,1
23	2x*sinx – cosx=y		[0,4; 1]	0,05
24			[-1; 0]	0,1
25	lnx – x + 1,8=y		[2; 3]	0,1
26			[0,2; 1]	0,05
27			[1; 2]	0,1
28			[1; 2]	0,1
29			[0; 1]	0,1
30	0,6*3x -2,3*x – 3=y		[2; 3]	0,1

Задание 3

Нахождение корней нелинейных (трансцендентных) уравнений, используя инструмент «Подбор параметра»

Пример. Найти корни уравнения

Из рис.1 видно, что функция меняет знак между значениями Xдиапазона [3,2;3,3]. Значит, в этом диапазоне существует корень. В качестве начального приближения Xкорень берем ячейку F3=3, значение функции Y задаем в ячейке F4=3*F3-4*ln(F3)-5.

Теперь выберем команду Сервис, Подбор параметра и заполним диалоговое окно Подбор параметра. Заполнение окна смотрите на рис.1.

После нажатия кнопки OK средство Подбора параметров находит приближенное значение корня, которое помещает в ячейку F3, а корень-результат в ячейку F4(смотрите рис.2).

Рис.1