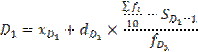Контрольная работа: Контрольная работа по Статистике 15

Таким образом, из 20 страховых организаций 30 % имеют 4 страховых случая, 25% - 5 страховых случаев, 20% - 3 страховых случая, 15% - 6 страховых случаев и 10% - 7 страховых случаев.

Самыми крупными являются вторая и третья группы, так как в них сосредоточено самое большое количество страховых организаций, поэтому эти же группы являются самыми крупными по числу договоров страхования. Наибольшее среднее количество договоров страхования соответствует группам с наибольшим количеством страховых случаев, таким образом, большее число договоров страхования соответствует большему числу страховых случаев. Такая же ситуация складывается, если посмотреть на средний размер страховых выплат: наибольший средний размер страховых взносов соответствует группам с большим количеством страховых случаев, то есть большее количество страховых случаев соответствует большему размеру страховых взносов, что обусловлено большим числом договоров страхования. Также и больший размер страховых выплат соответствует большему размеру страховых взносов, большему количеству страховых случаев и большему числу договоров страхования.

Задание 3. Имеются следующие данные о распределении вкладчиков банка по размеру вкладов:

Группы вкладчиков по размеру вкладов, Д.е.	Численность вкладчиков, в % к итогу
до 2000 2000 – 4000 4000 – 6000 6000 – 8000 8000 – 10 000 10 000 – 12 000 12 000 и более	2 3 8 10 15 32 30
Итого:	100

Определите:

· · средний размер вклада;

· · модальное значение признака;

· · уровень дифференциации вкладчиков по размеру вклада (как отношение девятого дециля к первому)

· · дисперсию способом моментов.

Решение.

1) В данной задаче интервалы открытые, их следует закрыть.

Средний размер вклада найдем по формуле средней арифметической взвешенной:

Для этого найдем середины интервалов. Так как данная частота появления признака представлена в процентах, то следует подсчитать относительное выражение частоты, то есть частость по формуле:

Поэтому формула средней арифметической взвешенной будет иметь вид:

Группы вкладчиков по размеру вкладов, д.е.	Численность вкладчиков, в % к итогу, fi	Середина интервала, д.е., х i	Частость, wi	х i wi	Накопленные частоты, Si
0 – 2000	2	1000	0,02	20	2
2000 – 4000	3	3000	0,03	90	5
4000 – 6000	8	5000	0,08	400	13
6000 – 8000	10	7000	0,1	700	23
8000 – 10000	15	9000	0,15	1350	38
10000 – 12000	32	11000	0,32	3520	70
12000 – 14000	30	13000	0,3	3900	100
Итого:	100	49000	1	9980

Таким образом, средний размер вклада составляет 9980 д.е.

2) Так как мода – это интервал с наибольшей частотой, то, чтобы определить модальный интервал, выбираем наибольшую частоту. Она равна 32. Следовательно, модальное значение признака находится в интервале от 10000 до 12000.

Значение моды находим по формуле:

Величина интервала d равна 2000.

Наиболее часто встречаются вкладчики с размером вклада 11789 д.е.

3) Найдем первый дециль. Для этого сначала находим интервал, в котором он находится, по формуле:

По накопленной частоте определяем интервал, в котором находится первый дециль – это интервал от 4000 до 6000. Находим значение первого дециля по формуле: