Контрольная работа: Лагові моделі. Метод Койка, Ш. Альмона

0.001 βо

…

0

Слід зазначити, що метод Койка має такі переваги:

- припускаючи, що λ можуть бути від'ємними, Койк абстрагувався від зміни знака коефіцієнта при β_і ;

- завдяки тому, що λ<1 віддалені за часом, значення β_і стали менш впливовими, ніж поточні;

- сума β_і , яка складає довгостроковий мультиплікатор, є скінченною, тобто

. (1.5)

як результат (1.4), модель з кінцевим лагом (1.5) можна записати таким чином:

. (1.6)

Як бачимо, модель (1.6) також незручна для оцінки, оскільки залишається дуже велика (фактично нескінченна) кількість оцінюваних параметрів, крім того, параметр λ входить до моделі в нелінійній формі: тобто метод лінійної (за параметрами) регресії не можна застосувати до цієї моделі. Але Койк пропонує модифікований метод, який полягає в тому, що в модель (1.6) вводиться затримка на один період. Виходячи з цього, модель записується таким чином:

. (1.7)

Далі помножуємо (1.7) на λ і отримаємо:

. (1.8)

Віднявши (1.8) від (1.6), маємо:

, (1.9)

або

, (1.10)

де . Ця процедура відома як перетворення Койка . Порівнюючи (1.10) з (1.3), бачимо надзвичайне спрощення моделі. Якщо раніше нам треба було оцінювати параметр αλ та нескінченну кількість параметрів β_і, тепер достатньо оцінити лише три змінних: α,β_о і λ, тобто немає причин очікувати мультиколінеарність. Фактично ми позбулись мультиколінеарності заміною х_t-1 , х_{t - 2} … на одну змінну, тобто у_{t -1} .

Зазначимо деякі особливості трансформації Койка.

1. Трансформація Койка переводить дистрибутивно-лагову модель в авторегресивну, оскільки серед незалежних змінних залишається у_{t -1} .

2. Поява у_{t -1} може спричинити ряд статистичних проблем: у_{t -1} , як і у_t , - стохастична; це означає, що в модель ми вводимо стохастичну змінну.

3. У початковій моделі (1.3) помилка дорівнювала ε_t , а в перетвореній . Тепер статистичні властивості υ_t залежать від статистичних властивостей ε_t .

4. Наявність лагового значення у порушує одне з припущень d-тесту Дарбіна-Уотсона. Отже, нам потрібно розробити альтернативу для тестування серійної кореляції при лаговому у. Цією альтернативою є h-тест Дарбіна.

Підхід Ш. Альмона до дистрибутивно-лагових моделей: поліноміальний лаг Альмона

Хоча дистрибутивно-лагова модель Койка широко використовується на практиці, вона базується на припущенні, що коефіцієнти β спадають у геометричній прогресії в міру зростання довжини лагу. Це припущення може бути занадто строгим у деяких ситуаціях, і схема дистрибутивно-лагових моделей Койка не спрацює. У складніших випадках параметри β_і можна виразити як функцію від і, тривалості лагу (часу) і підібрати відповідні криві, які відображатимуть цю функціональну залежність. Саме цей підхід і запропонований Ш.Альманом. Щоб проілюструвати його метод, повернемося до скінченної дистрибутивно-лагової моделі:

. (1.11)

ЇЇ можна записати в більш компактному вигляді:

. (1.12)

Відповідно до теореми Веєрштрасса Альмон припустив, що β_і можна апроксимувати поліномом відповідного ступеня від і, тривалості лагу. Наприклад:

. (1.13)

Щоб пояснити, як працює схема Альмона, припустимо, що β_і змінюються таким чином, що можна обрати поліноміальну апроксимацію другого ступеня (вигляд залежності краще за все обирати за зовнішнім виглядом графіка залежності величини параметра від лагу). Підставляючи (1.13) до (1.12), отримаємо:

. (1.14)

Визначаючи

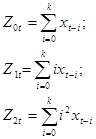(1.15)

можна переписати (1.14) як

. (1.16)

У моделі Альмона у залежить від штучно створених змінних Z, а не від початкових змінних х. Зауважимо, що (1.16) можна оцінити за звичайним методом найменших квадратів. Оцінки α і а_і , отримані таким чином, матимуть усі бажані статистичні властивості, якщо випадкова величина ε_t задовольнятиме припущенням класичної моделі лінійної регресії. З цього боку модель Альмона має чітку перевагу перед моделлю Койка

Перед застосуванням методу Альмона потрібно вирішити такі практичні проблеми.

1. Максимальна тривалість лагу k має бути визначена заздалегідь. Це найголовніший недолік методу Альмона. Дослідник повинен визначити найпридатнішу тривалість лагу. На практиці, звичайно, припускають, що k достатньо мала.

2. Визначивши k, треба також визначити ступінь полінома т. В загальному випадку ступінь полінома має бути принаймні на одиницю більший за кількість точок екстремума кривої, що показує залежність β_і від і. Тобто заздалегідь потрібно знати кількість точок екстремуму, таким чином, вибір т є великою мірою суб'єктивним. Але в деяких випадках теорія може допомогти знайти потрібний вигляд кривої. На практиці припускають, що за допомогою полінома низького ступеня (скажімо, т дорівнює 2 або 3) можна отримати добрі результати. Якщо ми обрали певне значення т і хочемо з'ясувати, чи не буде кращим поліном вищого ступеня, потрібно діяти таким чином.