Контрольная работа: Математические методы исследования в экономике
Цех хлебозавода по производству муки заключил контракт с мини-пекарней о поставке ежедневно 300 кг ржаной и пшеничной муки, причем пшеничной - не менее 50%. Зерно, поступающее в цех, проходит в нем обмолот, помол и упаковку муки. Трудозатраты (в человеко-часах) на указанные операции представлены в таблице:
| Операция | Ржаная мука | Пшеничная мука | Имеющийся ресурс |
| Обмолот | 0,1 | 0,1 | 30 |
| Помол | 0,1 | 0,08 | 27 |
| Упаковка | 0,05 | 0,05 | 200 |
Себестоимость одного килограмма ржаной муки составляет 14 рублей, а пшеничной - 18 рублей.
Требуется найти оптимальный план производства продукции, позволяющий цеху выполнить условия контракта с наименьшими затратами.
Решение.
Пусть x1 - объем производства ржаной муки, x2 - объем производства пшеничной муки. Тогда задача может быть описана в виде следующей модели линейного программирования:
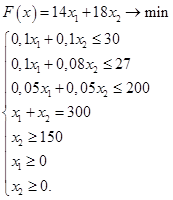
Заполним данные в среде MicrosoftExcel
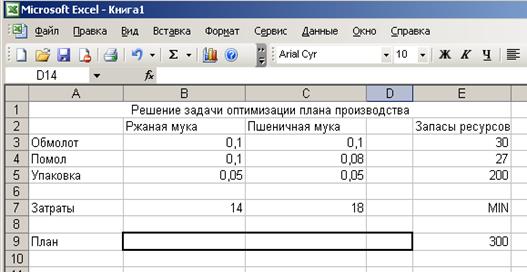
Добавим в таблицу еще одну строку (например, строку 9 План), в которую будут вноситься получаемые в ходе решения результаты. Объем производства ржаной муки будем предполагать получить в ячейке В9, пшеничной муки - в ячейке С9, а затраты на себестоимость - в ячейке D7.
Для решения задачи необходимо также выделить столбец (в данном примере - столбец D), в который будут введены формулы для расчета значений левой части ограничений. Формула вводится также и в ячейку, в которой будет рассчитаны затраты на себестоимость предприятия (ячейка D7). Нужно обратить внимание на то, что в формулах используются не числа или символьные обозначения, а координаты ячеек таблицы, в которых хранятся эти числа и переменные.
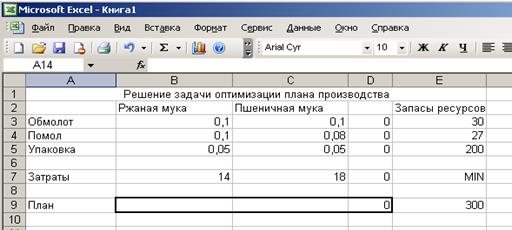
D3= СУММПРОИЗВ(B3:C3;$B$9:$C$9)
D4= СУММПРОИЗВ(B4:C4;$B$9:$C$9)
D5= СУММПРОИЗВ(B5:C5;$B$9:$C$9)
D7= СУММПРОИЗВ(B7:C7;$B$9:$C$9)
D9=B9+C9
Для запуска процедуры оптимизации в меню Сервис необходимо выбрать пункт Поиск решения. В поле Установить целевую ячейку вводятся координаты ячейки (D7), которую необходимо минимизировать.
В поле Изменяя ячейки вводятся координаты ячеек (разделенные запятыми или объединенные в интервал двоеточием), в которых содержатся значения переменных - объемов производства ржаной и пшеничной муки. Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. В поле Ограничения необходимо ввести все граничные условия задачи:
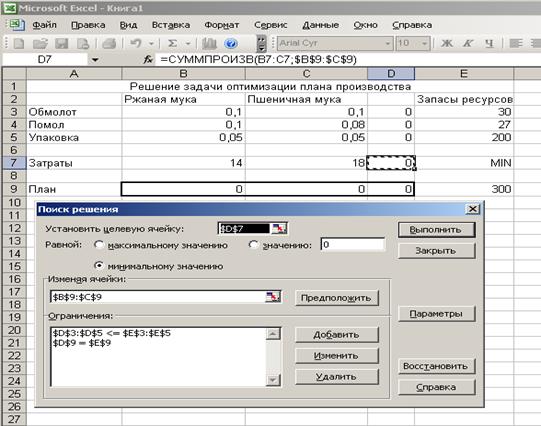
При этом ограничения на неотрицательность переменных можно ввести путем установки флажка Неотрицательные значения в окне Параметры. В случае, если решаемая задача является задачей линейного программирования, лучше отметить это в окне Параметры соответствующим флажком:
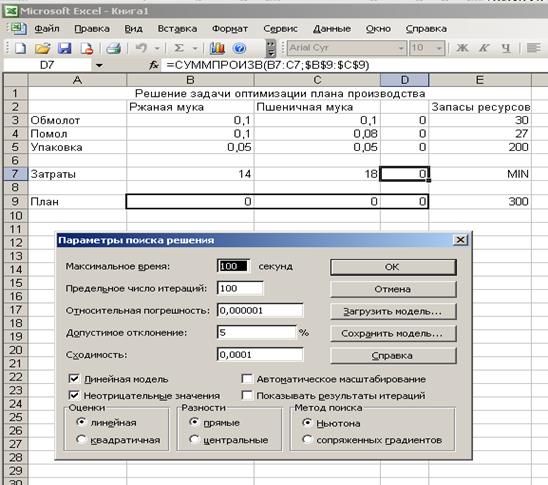
Запуск процесса оптимизации производится нажатием кнопки Выполнить. По окончании счета появляется диалоговое окно Результаты поиска решения. Нажав в нем соответствующую кнопку, можно сохранить найденное решение или восстановить исходные значения. Изменения при этом коснутся как целевой ячейки, так и влияющих ячеек. В этом же диалоговом окне можно указать необходимые типы отчетов, которые будут размещены на отдельных листах книги.
Отчет Результаты отражает исходные и результирующие значения целевой и влияющих ячеек, а также сведения о наложенных ограничениях.
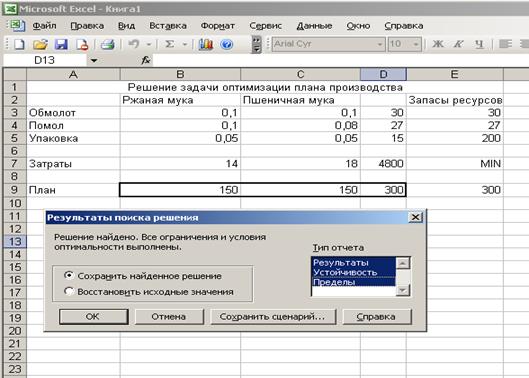
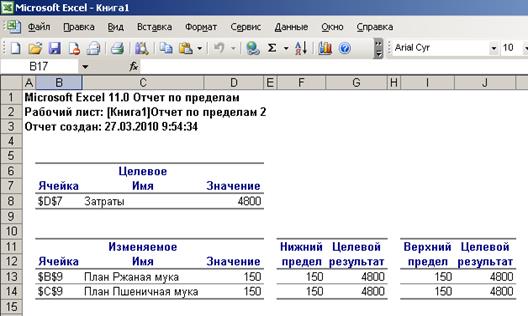
Таким образом предприятию необходимо выпустить 150 кг ржаной муки и 150 кг пшеничной муки, тогда минимальная себестоимость выпуска составит 4800 человеко-часов, при этом ресурсы на обмолот и помол будут использованы полностью, а ресурсы на упаковку останутся в избытке в количестве 185 человеко-часов.
Задача 2.2
Руководство птицефабрики имеет возможность закупать корма трех видов. Из этих кормов птицы должны получать питательные вещества (П1, П2, П3 и П4), требуемое количество которых и содержание в кормах (в ед.) приведены в таблице:
|
Питательные вещества | Корма | Нормы потребления | ||
| К1 | К2 | К3 | ||
| П1 | 3 | 5 | 0 | равно 16 |
| П2 | 2 | 2 | 4 | не менее 24 |
| П3 | 8 | 1 | 2 | не менее 25 |
| П4 | 4 | 3 | 5 | не менее 33, но не более 40 |
Цены за 1 т кормов составляют соответственно 1000, 900 и 800 рублей.
Какие корма и в каком количестве следует закупать, чтобы затраты птицефабрики оказались минимальными?
Решение.
Решение: обозначим за x1 количество корма К1, за x2 - количество корма К2, за x3 - количество корма К3. Тогда:
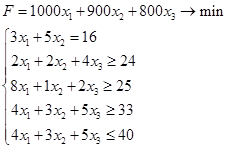
Подготовим в MicrosoftExcel таблицу для решения задачи:
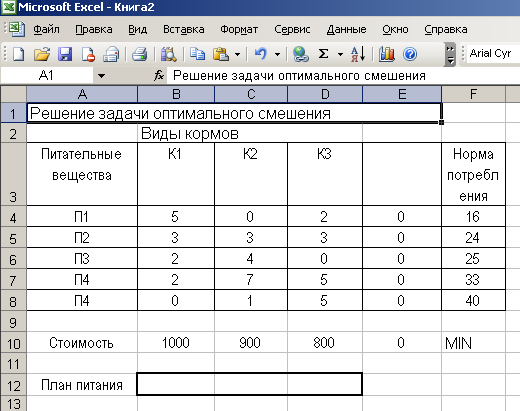
Поскольку MicrosoftExcel позволяет путем установки соответствующего флажка автоматически определять неотрицательность переменных, добавление ограничений на неотрицательность в модель при решении задачи в MicrosoftExcel не является обязательным.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--