Контрольная работа: Математические последовательности Предел функции

Задание 1

Вычислите и последовательности .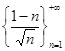

Решение.

Рассмотрим последовательность .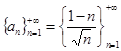

для любого натурального

Следовательно, множество 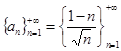является ограниченным сверху. Это означает, что последовательность 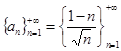имеет верхнюю точную грань: .

Следовательно, множество 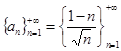не является ограниченным снизу. Это означает, что нижняя грань последовательности 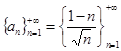не существует.

Ответ. 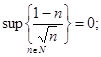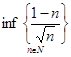не существует

Задание 2

Пользуясь определением предела последовательности, докажите, что .

Доказательство.

Число называется пределом последовательности , если для любого положительного числа существует номер такой, что при выполняется неравенство .

Используя определение предела последовательности, докажем, что .

Возьмем любое число .

Если взять , то для всех будет выполняться неравенство . Следовательно, .

Доказано

Задание 3

Пользуясь определением предела функции, докажите, что .

Доказательство

Число называется пределом функции при , если для любого числа существует число такое, что для всех , удовлетворяющих неравенству , выполняется неравенство .

Используя определение предела функции, докажем, что .

Возьмем любое .

Положим .

--> ЧИТАТЬ ПОЛНОСТЬЮ <--