ЗМІСТ

Вступ.. 2

1.Заміна площин проекцій.. 3

2. Плоскопаралельне переміщення.. 5

3.Обертання навколо ліній рівня.. 7

4. Косокутне допоміжне проектування.. 10

Висновки.. 11

Список літератури.. 12

Вступ

Розділ геометрії, в якому просторові фігури ( оригінали вивчають за допомогою зображень їхніх графічних моделей на площині малюнка називають нарисною геометрією.

Малюнок повинен нести геометричну інформацію про форму та розміри оригіналу, бути наочним, простим і точним. Формоутворюючими елементами простору є основні геометричні фігури – точка, пряма та площина, з яких утворюються складніші фігури. Геометричною фігурою називають будь – яку непусту множину точок, а геометричний простір може складатися з множини точок, прямих чи площин. Основою нарисної геометрії є метод проекцій, який дає можливість одержувати відображення просторових фігур на площині чи поверхні. За цим методом кожній точці тривимірного простору відповідає певна точка двовимірного простору ( площини ). На площині зображують усі фігури, розміщені в просторі. Перетин проектуючого променя з площиною проекцій дає проекцію точки. Проекцією прямої в загальному випадку є пряма, що проходить через точку її перетину з площиною проекцій. Малюнок, що складається з кількох (мінімум двох) зв'язаних між собою проекцій зображуваної фігури називають комплексним малюнком.

1.Заміна площин проекцій

На Мал. 1,а в системі площин проекцій і зображено точку А. Перпендикулярно до площини проводять нову вертикальну площину , на яку ортогонально проектують точку А. Таким чином, замість системи площин проекцій / з проекціями точки одержують систему / з проекціями точки . При такій заміні відстань від старої проекції до старої осі дорівнює відстані від нової проекції до нової осі. На комплексному рисунку (Мал. 1, б) ці відстані позначено двома рисками. [1] [2]

Мал. 1

На Мал. 2 зображено відрізок прямої загального положення АВ. Щоб одержати його натуральну величину, досить провести нову площину паралельно одній з проекцій ( на рисунку вісь паралельна горизонтальній проекції прямої). Відклавши від нової осі відповідні відстані від фронтальних проекцій точок до старої осі, одержують натуральну величину відрізка .[1]

Мал. 2

Для розв’язання ряду метричних задач пряму необхідно поставити в проектуюче положення. Для цього треба скористатися натуральною величиною відрізка. Якщо провести площину, перпендикулярну до неї ( її слід – вісь ), то відклавши відстань, позначену двома рисками, одержимо проекцію прямої у вигляді точки .

На Мал. 3 показано визначення відстані між відрізками двох мимобіжних прямих - і . Для цього подвійною заміною площин проекцій пряму проектують в точку, а пряма спроектувалась при цьому у відрізок . Перпендикуляр, опущений з на дає шукану відстань.

Мал. 3

Крім визначення відстані можна тут же визначити дві найближчі точки і на мимобіжних прямих. Показано визначення точок і . А далі в зворотному напрямі можна визначити точки і на полях та

На Мал. 4 показано визначення натуральної величини трикутного відсіку подвійною заміною площин проекцій. Для цього в площині трикутника спочатку проведено горизонталь . Перпендикулярно до горизонтальної проекції горизонталі вибирають вертикальну площину ( її горизонтальний слід - ), При цьому горизонталь спроектувалася в точку , а весь відсік – у пряму . Паралельно прямій проводять слід площини і визначають натуральну величину трикутного відсіку.[1], [2]

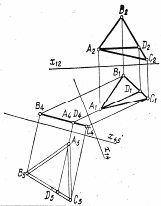
Мал. 4

2. Плоскопаралельне переміщення

Якщо при способі заміни площин проекцій геометричні фігури залишаються на місці, а до них певним чином підбирають площини проекцій, то при способі плоскопаралельного переміщення роблять навпаки: площини проекцій і залишають незмінними, а геометричні фігури переміщують певним чином. [1], [3]

На Мал. 5а зображено відрізок прямої загального положення . Для визначення натуральної величини відрізка через його кінцеву точку проводять вертикальну вісь , навколо якої відрізок повертають до фронтального положення. Точка при цьому переміщується по дузі кола, площина якого перпендикулярна до вертикальної осі , а отже, і горизонтальна. Натуральну величину показано подвійною прямою ()

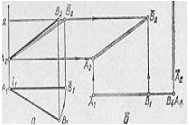
Мал. 5

--> ЧИТАТЬ ПОЛНОСТЬЮ <--