Контрольная работа: Методика регрессионного анализа

Проверка коэффициентов уравнения регрессии на статистическую значимость проводиться с помощью t -критерия:

Для значения α = 0,05, получим α/2 = 0,025 и значение t-критерия Стьюдента равно . Поскольку в матрице дисперсий-ковариаций не нулевые только диагональные элементы и равны между собой (), то все доверительные интервалы равны между собой:

Теперь проверим все коэффициенты на статистическую значимость исходя из условия: если – то коэффициент статистически значим, если – то коэффициент статистически не значим.

коэффициент	b0	b1	b2	b3	b4	b5	b6	b7
	36,542	23,292	13,625	10,458	1,375	2,375	5,208	1,875
Статистически значим	+	+	+	+	-	+	+	-

Таким образом мы получили, что коэффициенты b ₄ и b ₇ – статически не значимы, поэтому мы не будем вносить их в нашу модель. И окончательный вид модели будет таким:

Число = 6 – количество эффектов, которые вошли в структуру модели, то есть статистически значимые.

Значения откликов, полученных с помощью последней модели:

Отклик	y1	y2	y3	y4	y5	y6	y7	y8
	-3.25	38.584	13.584	55.418	2.5	53.834	40.166	91.5
	3.25	3.251	3.251	3.249	0.5	0.499	0.501	0.5

Проверка модели на адекватность производиться с использованием F -критерия Фишера:

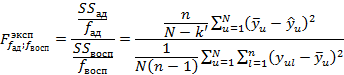
Где – числа степеней свободы для и :

Просчитаем экспериментальное значение:

По таблицам значения критерия Фишера (приложения 3) для q = 0,05 находим:

Так как выполняется условие значит модель адекватна.

Так как у нас , то нет необходимости определять значимость обратного отношения дисперсий.

Проверка на информативность [1, с. 97-99]

Коэффициент множественной корреляции R определяется по формуле:

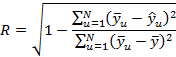
Посчитанное значение R = 0,997 которое очень близко к единице.

Гипотезу о значимости множественного коэффициента корреляции проверяют по F -критерию:

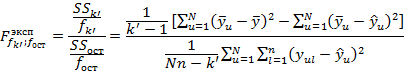
Где – суммы квадратов отклонений – связанная с коэффициентом модели и остаточная; – числа степеней свободы для и .

В нашем случае: