Контрольная работа: Методы математической статистики

DX₁ DX₂ . . . DX_n

5. Метод наибольшего правдоподобия для нахождения оценок параметров плотности распределения

Метод наибольшего правдоподобия основывается на представлении выборки объема n как n-мерной случайной величине (Х₁ , Х₂ , ..., Х_n ), где рассматриваются как независимые случайные величины с одинаковой плотностью распределения f(x). Плотность распределения такой n-мерной случайной величины называется функцией правдоподобия L(x₁ , x₂ , ..., x_n ), которая в силу независимости случайных величин равна произведению плотностей распределения случайных величин Х₁ , Х₂ , ..., Х_n :

L(x₁ , x₂ , ..., x_n ) = f(x₁ ) f(x₂ )... f(x_n ).

Отсюда следует, что всякую функцию у=у(x₁ , x₂ , ..., x_n ) выборочных значений x₁ , x₂ , ..., x_n , называемую статистикой, можно представить как случайную величину, распределение которой однозначно определяется функцией правдоподобия.

Рассмотрим метод отыскания оценок параметров по опытным данным, который использует функцию правдоподобия.

Пусть f(x;а) – плотность распределения случайной величины Х (генеральной совокупности), зависящей от параметра а. Функция правдоподобия также будет зависеть от параметра а и иметь вид

Сущность метода наибольшего правдоподобия заключается в том, чтобы найти такое значение параметра а, при котором функция правдоподобия L(x₁ , x₂ , ..., x_n , а) была бы максимальной. Для этого необходимо решить уравнение

и найти то значение а, при котором функция L(x₁ , x₂ , ..., x_n , а) достигает максимума. С целью упрощения вычисления обычно максимизируют натуральный логарифм функции правдоподобия, пользуясь тем, что

Если неизвестными являются несколько параметров а₁ , а₂ , ... , а_m , то функция правдоподобия зависит от m переменных L = L(x₁ , x₂ , ..., x_n ; а₁ , а₂ , ... , а_m ) и решаются m уравнений

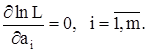
Пример. Пусть на вход приемного устройства поступает сумма двух сигналов: Y(t) = X + Z(t), где Х – неизвестный не зависящий от времени сигнал, а Z(t) – случайная помеха. В моменты времени t₁ , t₂ , ... , t_n производятся измерения величины Y(t). На основании опытных данных (выборки) y₁ = y(t₁ ), y_{2 =} y(t₂ ), ... , y_n =y(t_n ) нужно найти приближенное значение сигнала Х.

Решение. Пусть Z(t₁ ), Z(t₂ ), ... , Z(t_n ) – независимые случайные величины распределены по нормальному закону с математическим ожиданием m_Z = 0 и дисперсией D(Z) = s² . Тогда случайные величины также независимы, нормально распределены с неизвестным математическим ожиданием а и с той же дисперсией s² . Плотность распределения случайных величин Y(t₁ ), Y(t₂ ), ... , Y(t_n ) имеет, таким образом, вид

Запишем функцию правдоподобия для n-мерной случайной величины (Y₁ , Y₂ , ... , Y_n ):

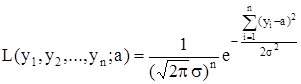
Tак как

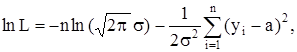
то из уравнения

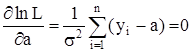
Имеем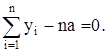

Значит

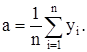
Нетрудно показать, что функция правдоподобия L = L(y₁ , y₂ , ..., y_n ; а) при этом а достигает своего максимума. Таким образом мы показали, что оценка математического ожидания неизвестного сигнала Х по методу наибольшего правдоподобия в предположении нормального распределения аддитивной помехи является средним арифметическим измерений y₁ , y₂ , ..., y_n :

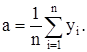
Метод наибольшего правдоподобия обладает важным свойством: он всегда приводит к состоятельным, хотя иногда и к смещенным, и эффективным оценкам.

На практике использование метода наибольшего правдоподобия часто приводит к необходимости решать достаточно сложные системы уравнений.

6. Метод наименьших квадратов

математическая статистика метод распределение выборка