Контрольная работа: Модели и методы принятия решений

Нет

Нет

Да

Да

Нет

Нет

Из таблицы видно, что имеется два оптимальных маршрута следования коммивояжера А₀ А₄ А₃ А₂ А₁ А₀ и А₀ А₁ А₂ А₃ А₄ А₀ , имеющие минимальную из всех возможных маршрутов длину, равную 720 км.

2. ДИНАМИЧЕСКАЯ ОПТИМИЗАЦИЯ В ПЛАНИРОВАНИИ РАБОТ

Задача 1.10

В условиях задачи производственного планирования (см. МУ [12]) найти оптимальные строки начала строительства каждого из объектов так, чтобы суммарный срок строительства всех объектов был бы минимальным.

Таблица 1.10.10 – Исходные данные

Объекты	Виды (стадии) работ
	1	2	3	4
А1	1	2	5	2
А2	3	2	3	4
А3	2	5	2	4

Решение

Считая, что работа на каждом объекте должна продолжаться непрерывно с момента начала строительства до его окончания, требуется определить сроки начала строительства каждого объекта так, чтобы суммарный срок строительства всех объектов был минимальным.

Последовательность строительства может быть любой:

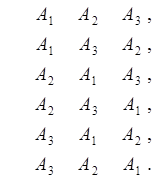
Покажем, как оценивается суммарное время строительства для одного из вариантов, например А₁ А₂ А₃ . Сроки окончания работ на первом объекте будут следующими (см. табл. 1.10.10):

-окончание первой стадии 1 месяц;

-окончание второй стадии 1 + 2 = 3 месяца;

-окончание третьей стадии 3 + 5 = 8 месяцев;

окончание четвертой стадии 8 + 2 = 10 месяцев.

Время t₂ начала работ на втором объекте должно удовлетворять следующим неравенствам:

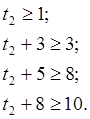
Эти неравенства выражают требования, чтобы каждая из стадий работ на объекте А₂ начиналась лишь после окончания работ соответствующих стадий на объекте А₁ . Одновременно (параллельно) вести один и тот же вид работ у организации нет возможности но условию задачи.

Первое неравенство выражает требование, чтобы первая стадия работ на втором объекте начиналась лишь после окончания первой стадии работ на первом объекте, т.е. через один месяц.

Второе неравенство выражает требование, чтобы вторая стадия работ на втором объекте начиналась лишь после окончания второй стадии работ на первом объекте, т.е. через четыре месяца. При этом надо помнить, что первая стадия работ на втором объекте уже выполнена (t₂ +3).

Третье неравенство выражает требование, чтобы третья стадия работ на втором объекте начиналась лишь после окончания третьей стадии работ на первом объекте, т.е. через восемь месяцев (первая и вторая стадии работ на втором объекте уже выполнены, следовательно, t₂ +5).

Четвертое неравенство выражает требование, чтобы четвертая стадия работ на втором объекте начиналась лишь после окончания четвертой стадии работ на первом объекте, т.е. через десять месяцев (первая, вторая и третья стадии работ на втором объекте выполнены, следовательно, t₂ + 8).

Наименьшее значение t₂ , удовлетворяющее этим неравенствам, равно 3. Поэтому самый ранний возможный срок начала строительства второго объекта А₂ три месяца после начала строительства первого объекта А₁ . Зная это значение, несложно определить сроки окончания соответствующих стадий работ:

окончание первой стадии 3 + 3 = 6 месяцев;