Контрольная работа: Моделирование машины Тьюринга

Выполнил:

студент группы АСУ-21

Мустафин Ш. Р.

Проверил:

преподаватель

Минаев С.В.

Саратов 2010

Цель

Изучение принципов работы машины Тьюринга, приобретение практических навыков программирования машины Тьюринга.

Задание

Изучить правила написания алгоритмов на эмуляторе машины Тьюринга;

Получить у преподавателя вариант задания для реализации алгоритма;

Разработать алгоритм в соответствии с полученным заданием;

Отладить написанный алгоритм на эмуляторе машины Тьюринга.

Задача

Сложение нескольких чисел в двоичной системе.

Описание метода решения

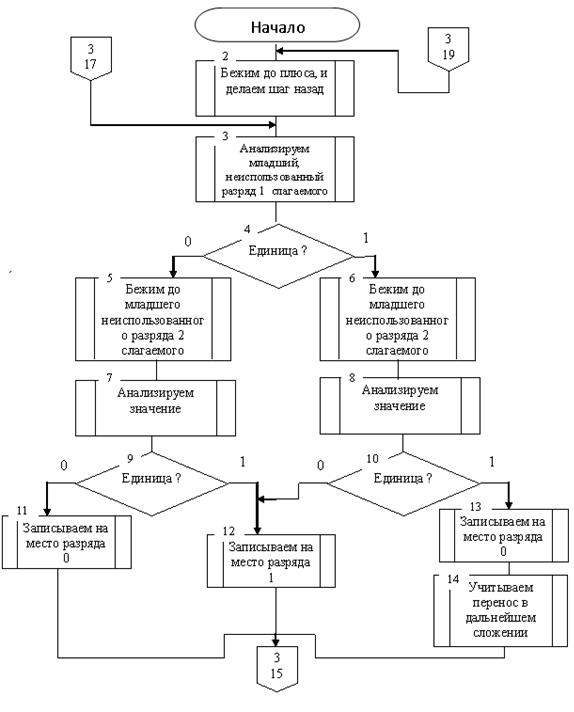
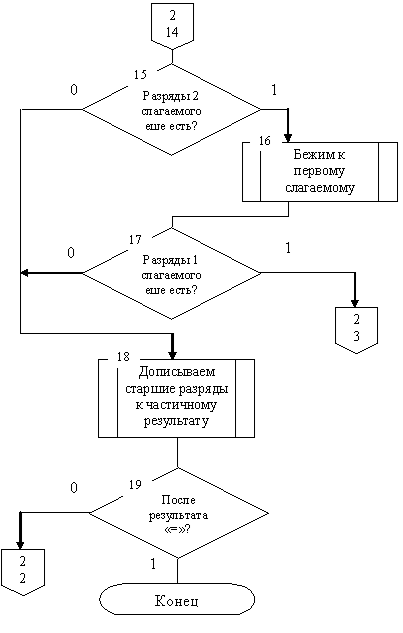
Для более удобной реализации алгоритма на эмуляторе, сложение будет выполняться поэтапно. Сначала будем складывать два первых слагаемых, затем результат этого сложения с третьим и так далее, пока не дойдем до знака «=». Первым шагом ищется самый младший, неиспользованный разряд первого слагаемого. В зависимости от его значения переходим в следующие соответствующие состояния. Далее ищем самый младший, неиспользованный разряд второго слагаемого и записываем на его место результат сложения этих двух разрядов. Затем снова возвращаемся на первый шаг. Этот цикл осуществляется до тех пор, пока у одного из слагаемых не кончатся разряды. Записываем оставшиеся старшие разряды к результату, с учетом переноса, если он есть. Стираем лишние символы, находящиеся до старших разрядов результата. Проверяем какой знак стоит после результата. Если «+», то возвращаемся к первому шагу, если «=», то конец подсчетам.

Описание программы

Для удобства в программе все 1 и 0 заменяются на I и O соотвественно. Далее состояние q5 доходит до + и переходит в состояние q6, в зависимости от того, какой символ стоит перед + q6 переходит в q16 – i, q15 – o. q16, q7, q9 – это состояния которые несут единицу во второе слагаемое без переноса, и в зависимости от значения, записывают в самый младший, неиспользованный разряд результат сложения. Если переноса нет, то переходим в состояние q11, есть – q10. Q11,q13 – бегут к первому слагаемому и анализируют самый младший, неиспользованный разряд и в зависимости от значения переходят в состояния q16 и q15, если разрядов нету, то в q14. Q14 и q17 затирают ненужные символы и переходят в состояние q6. Q15, q37,q39 - это состояния которые несут ноль во второе слагаемое без переноса, и в зависимости от значения, записывают в самый младший, неиспользованный разряд результат сложения и переходят в состояние q11. Q10,q23 – бегут с переносом к первому слагаемому и анализируют самый младший, неиспользованный разряд и в зависимости от значения переходят в состояния q16 и q26, если разрядов нету, то в q24. Q26 аналог q15, только несет значение 0 с переносом. Q24 аналог q14, но с учетом переноса. Программа останавливается, когда одно из состояний, преобразую частичную сумму, после младшего разряда находит символ «=».

Алгоритм решения

Код программы

[MoT Data]

1110111+111111+10101010101010101010+…++11=

q1s q1s dR

q1s1q1sidR

q1s0q1sodR

q1s+q1s+dR

--> ЧИТАТЬ ПОЛНОСТЬЮ <--