Контрольная работа: Основные понятия космической геодезии и астрономии

В результате первого этапа орбита определяется в виде конического сечения (эллипса, иногда также параболы или гиперболы), в фокусе которого находится другое (центральное) тело. Такие орбиты называются невозмущёнными или кеплеровыми, т.к. движение небесного тела по ним происходит по законам Кеплера.

Напомним:

Первый закон Кеплера (Закон эллипсов)

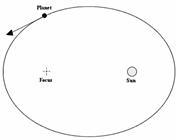
Каждая планета Солнечной системы обращается по эллипсy, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением

,

где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.

Закон всемирного тяготения Ньютона гласит, что «каждый объект во вселенной притягивает каждый другой объект по линии соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму

Вспомним, что в полярных координатах

В координатной форме запишем

Подставляя и во второе уравнение, получим

которое упрощается

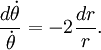
После интегрирования запишем выражение

для некоторой константы , которая является удельным угловым моментом ().Пусть

Уравнение движения в направлении становится равным