В гражданском законодательстве говорится, что гражданские права и обязанности возникают из предусмотренных законом оснований.

В судебной практике дело может стать предметом судебного разбирательства, если для этого есть достаточные основания. Приговор или решение суда должны быть мотивированными, т.е. обоснованными.

В повседневной речи, говоря о том, что многие законы не действуют, мы приводим в качестве основания то, что нет процедуры их использования и т.д.

Заключение

Рассмотренные выше основные формально-логические законы мышления открыты традиционной логикой. Как относится к ним символическая логика? Она основывается на них в своих построениях и процедурах, но в целях решения собственных специфических задач вносит в них необходимые уточнения и дает им свою символику. Так, раскрывая их единство в определенном отношении, она рассматривает их в качестве тождественно-истинных формул . Что это значит? Многие логические формулы, используемые в символической логике (логике высказываний), оказываются при одних логических значениях своих переменных истинными, а при других – ложными. Тождественно истинные формулы тем и отличаются, что они имеют логическое значение «истина» при всех логических значениях своих переменных. Истинность таких формул обусловлена их логической структурой. Поэтому они называются еще логически истинными формулами. В конечном счете их истинность определяется тем, что в их структуре отражаются наиболее глубокие и общие связи самого объективного мира. Посредством этих формул и выражаются законы логики.

Так, закон тождества выражается логической формулой А ≡ А (А равносильно А) или А->А («Если А, то А»).

Закон противоречия выражается формулой ┐ (А^ ┐А) («Неверно, что А и не-А).

Закон исключенного третьего – A v ┐А (А или не-А).

Считается, что закон достаточного основания символически выразить нельзя, так как это исключительно содержательный закон. Приведем пример толкования подобных формул. Так, сложные высказывания типа: «Закон принят, или закон не принят», «Решение суда правильное, или решение суда неправильное», имея формулу Av┐А (закон исключенного третьего), истинны независимо от того, истинны или ложны образующие их элементарные суждения. Вот таблица истинности этой формулы:

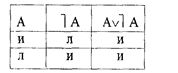
Наряду с тождественно-истинными формулами есть еще тождественно-ложные формулы. Ими выражаются логические противоречия.

Благодаря табличному способу символическая логика (логика высказываний) в состоянии эффективно выявлять как тождественно-истинные формулы, так и тождественно-ложные формулы – законы логики и логические противоречия. В этом ее громадный шаг вперед по сравнению с традиционной логикой.

Список используемой литературы

1. Логика. Учеб. Под ред. Иванова Е.И., Москва, 2000 г.

2. Аристотель. Соч. т. 1 с. 141, т. 2 с. 257.

3. Лейбниц Г. Избранные философские сочинения. М. 1968 с. 377.

4. Философские науки 1992 №1 с. 7

5. А.Д. Гетманова Учеб. 12-е издание, Москва, 2007 г.