Контрольная работа: Основы работы с редакторами MS Word, MS Excel и Visual Basic
Задача 1
Найти корни квадратного уравнения Ах2 + Вх + С = 0 по соотношениям X 1 = (- B + D )/ A /2 ; X 2 = - ( B + D )/ A /2, где D =( B 2 -4 AC )0.5
Лист Excel:
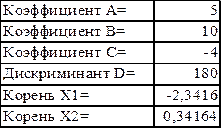
Таблица word (использованием макросов):
| Коэффициент А= | |
| Коэффициент В= | |
| Коэффициент С= | |
| Дискриминант D= | |
| Корень Х1= | |
| Корень Х2= |
Таблица Word (использование меню Таблица - Формула, при изменении входных данных для обновления результатов необходимо в контекстном меню результатов выбрать строку Обновить поле)
| Коэффициент А= | 5 |
| Коэффициент В= | 10 |
| Коэффициент С= | -4 |
| Дискриминант D= | 180 |
| Корень Х1= | -2,342 |
| Корень Х2= | 0,342 |
Формулы сокращенного умножения:
Гиперссылки на файл , место РІ документе , электронную почту.
Задача – Вычисление параметров треугольника
| Исходные данные: | |
| Сторона А= | 4 |
| Сторона B= | 6 |
| Сторона C= | 5 |
| Результаты: | |
Косинус угла  | 0,75 |
Косинус угла  | 0,12 |
Косинус угла  | 0,56 |
| Периметр | 15 |
| Площадь | 9,922 |
Задача 2
Создайте ведомость любого содержания с помощью таблиц редактора Word . (ведомость на выдачу заработной платы.)
| Минимальный оклад | Отчисления в фонды | Подоходный налог | ||||
| 132 | 1 | 13 | ||||
| Фамилия | Год рожден. | Разряд | Начислить | В фонды | Налоги | К выдаче |
| Репка | 2004 | 12 | 1584 | 15,84 | 205,92 | 1362,24 |
| Бабка | 1948 | 11 | 1452 | 14,52 | 188,76 | 1248,72 |
| Дедка | 1940 | 17 | 2244 | 22,44 | 291,72 | 1929,84 |
| Внучка | 1980 | 15 | 1980 | 19,8 | 257,4 | 1702,8 |
| Жучка | 1999 | 8 | 1056 | 10,56 | 15,84 | 1029,6 |
| Мышка | 2003 | 3 | 396 | 3,96 | 51,48 | 340,56 |
Задача 3
Запишите макрорекордером код любой операции форматирования текста.
или меню Сервис - Макрос… - Макросы - Макрос1 - Выполнить.
Задача 4
Вычисление расстояний от точки прямой линии до плоскости; вычисление расстояния между плоскостями.
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из точки на плоскость. Расстояние от точки М(х1 , y1 , z1 ) до плоскости Ax + By + Cz + D = 0 вычисляется по формуле
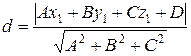
Расстояние между плоскостями 
и 
можно определить как расстояние между прямыми, лежащими в этих плоскостях и заданными своими направляющими векторами 
, 
и точками, через которые они проходят 
, 
соответственно. Известно, что прямая лежит на плоскости тогда и только тогда, когда
.
Координаты точек можно взять такими:
.
Расстояние между прямыми находят по формуле
.
С учётом того, что известны уравнения плоскостей (коэффициенты), получим следующий вид формулы:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--