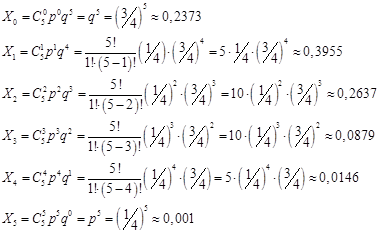Контрольная работа: Основы теории вероятностей

Вероятность появления непогашенной марки из первой совокупности равна , т.к. все марки, первоначально содержащиеся в альбоме, непогашенные, а из второй .

Вероятность того, что извлеченная наугад марка принадлежит первой совокупности , где - кол-во вариантов благоприятствующих событию (100 марок в первой совокупности), и - общее кол-во вариантов (100 марок плюс одна переложенная из первого альбома). Аналогично вероятность того, что извлеченная наугад марка принадлежит второй совокупности

Используя формулу полной вероятности, получим:

Ответ:

3. Что вероятнее: при бросании четырех игральных костей хотя бы на одной получить единицу, или при 24-х бросаниях двух игральных костей хотя бы раз получить две единицы?

Решение

Обозначим А событие – при бросании четырех игральных костей хотя бы на одной выпадет единица.

Вероятность выпадения единицы для всех костей одинакова и равна , соответственно вероятность выпадения другого числа равна .

Событие А подразумевает выпадение единицы на одной игральной кости или на двух, на трех, на четырех. Обратным для данного события будет событие, при котором ни на одной игральной кости не выпадет единицы. Найдем вероятность данного события. Выпадение числа отличного от единицы на каждом из 4ех кубиков это независимые события, поэтому применить теорему умножения, получим:

Вероятность события А равна:

Событие В – при 24х бросаниях 2х костей хотя бы раз выпадет две единицы.

Вероятность выпадения двух единиц равна , вероятность выпадения одной или нуля единиц равна .

Для вычисления вероятности появления события В так же удобно найти вероятность обратного события, т.е. вероятность события при котором ни в одном испытании не выпаде двух единиц. Для вычисления вероятности воспользуемся формулой Бернулли:

Итак,

Вероятность события В равна:

Ответ: событие А вероятнее.

4. Каждый из пяти студентов может с одинаковой вероятностью сесть в любой из четырех идущих друг за другом автобусов. Построить ряд распределения, найти функцию распределения, математическое ожидание и среднее квадратическое отклонение числа студентов, севших в первый автобус. Найти вероятность того, что: а) в первый автобус сел хотя бы один студент, б) в первый автобус село не более трех студентов.

Решение

Вероятность студента сесть в один из 4х автобусов равна , вероятность для всех студентов одинакова, .

Построим ряд распределения случайной величины Х - число студентов, севших в первый автобус.

Вычислим вероятность для каждого , используя формулу Бернулли: