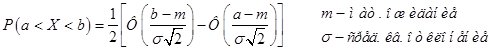Контрольная работа: Основы теории вероятностей

Найдем математическое ожидание по формуле:

Дисперсию найдем по формуле:

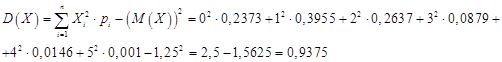
Среднеквадратическое отклонение:

а) вероятность того, что в первый автобус сел хотя бы один студент:

сумма вероятностей ряда распределения равна единице, поэтому допустимо вычислить вероятность от обратного(в автобус не село ни одного студента).

б) вероятность того, что в первый автобус село не более трех студентов:можно рассмотреть событие: в автобус не село 4 или 5 студентов.

5. Распределение случайной величины X определяется плотностью распределения вероятностей (распределение Лапласа):. Найти функцию распределения вероятностей F(x) и построить графики функций f(x) и F(x). Найти M(X), D(X) и σ. Вычислить вероятность попадания случайной величины X в промежуток .

Решение

По определению функция распределения — это интеграл от плотности распределения:

Для интегрирования необходимо рассмотреть два случая: и

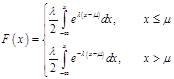
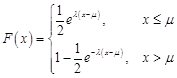
Графики функций для

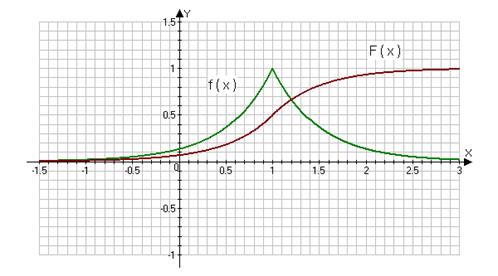
Математическое ожидание и дисперсия

В показателе экспоненты функции плотности содержится модуль разности, поэтому интервал необходимо разбить на и . Интегралы берутся по частям, при подстановке бесконечностей рассматриваются пределы вида .

Мат. ожидание:

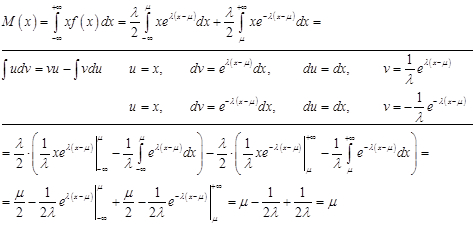
Дисперсия:

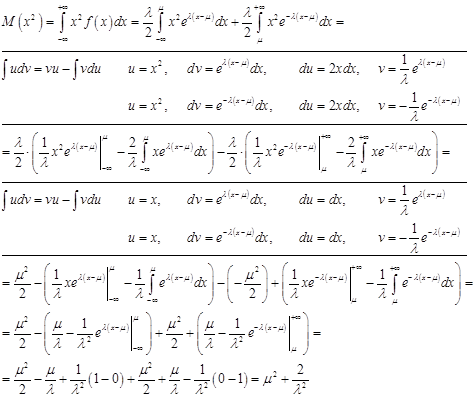
Вычислим вероятность попадания случайной величины X в промежуток :