Контрольная работа: Особенности решения задач в эконометрике
Следовательно, качество модели высокое.
Найдем величину средней ошибки аппроксимации А i .
Предварительно из уравнения регрессии определим теоретические значения 
для каждого значения фактора.
Ошибка аппроксимации А i , i =1…15:
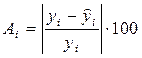
Средняя ошибка аппроксимации:
Ошибка небольшая, качество модели высокое.
2.2.4.Определим средний коэффициент эластичности:
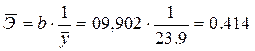
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,414%.
2.2.5.Оценим статистическую значимость полученного уравнения. Проверим гипотезу H 0 , что выявленная зависимость у от х носит случайный характер, т.е. полученное уравнение статистически незначимо. Примем α=0,05.
Найдем табличное (критическое) значение F -критерия Фишера:
Найдем фактическое значение F -критерия Фишера:
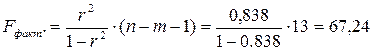
следовательно, гипотеза H 0 отвергается, принимается альтернативная гипотеза H 1 : с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x и y неслучайна.
Построим уравнение регрессии на поле корреляции
2.3. Модель степенной парной регрессии.
2.3.1. Рассчитаем параметры а и b степенной регрессии:
Расчету параметров предшествует процедура линеаризации данного уравнения:
и замена переменных:
Y=lny, X=lnx, A=lna