Контрольная работа: Параметры и силы, влияющие на вагон при движении

Поскольку угол q мал, то tgq»0, т.е. M₀ =Rh_M q, где R = R₁ + R₂ = Q, то приравнивая момент силы R₁ и R₂ моменту от их равнодействующей R, получим qh_M G = 2b2e_c q, отсюда

где f_ст – статический прогиб рессорного подвешивания вагона;

b – половина базы тележки.

Высота метацентра выше центра тяжести вагона более чем на 2 м, следовательно вагон устойчив.

4. Составление дифференциального уравнения вынужденных колебаний подпрыгивания вагона и нахождение аналитического выражения описывающего процесс вынужденных колебаний подпрыгивания вагона

Решение дифференциального уравнения n = 2p/Т является аналитическим выражением процесса вынужденных колебаний подпрыгивания вагона при движении его по регулярным неровностям вида z = hcoswt.

Это решение имеет вид:

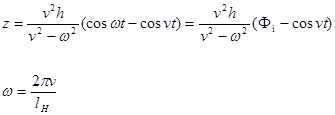
где n - скорость движения вагона;

l_н – длинна периода неровностей;

2h – высота неровностей;

n - круговая частота собственных колебаний

Для колеса вагона номер i возмущение функции имеет вид:

где l_i – расстояние от первого до i-го колеса.

Амплитуда вынужденных колебаний подпрыгивания кузова вагона будет иметь вид:

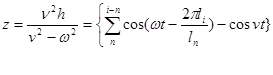
Для заданного вагона

Аналитическое выражение описывающее процесс вынужденных колебаний будет иметь вид:

Для построения графика определяем зависимость z от t

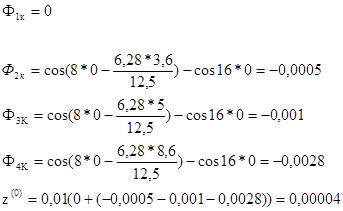
При t=1 сек

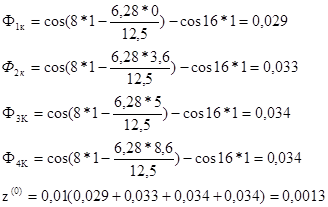
Для других значений t

ЧАСТЬ II

1. Расчет динамических боковых и рамных сил при вписывании вагона в кривых участках пути

Наибольшие боковые силы возникают тогда, когда при движении вагона наибольшее допустимое непогашенное ускорение на вагон достигает 0,7 м/с² . Это возможно при минимально допустимом для этой кривой возвышении наружного рельса. Его можно определить используя формулу: