Контрольная работа: Перетворення координат, операції масштабування в бібліотеці Opengl

Задамо якусь двовимірну систему координат (х, у). Афінне перетворення на площині описується формулами

де А, В, ..., F — константи. Значення (X, Y) можна розглядати як координати в новій системі координат.

Обернене перетворення (X, Y) у (х, у) також є афінним:

Афінне перетворення зручно записувати в матричному вигляді. Константи А, В, .... F утворюють матрицю перетворення, котра, будучи помножена на матрицю-стовпець координат (х, у) дає матрицю-стовпець (X, У). Однак щоб урахувати константи С та F, необхідно перейти до так званих однорідних координат — додамо ще один рядок у матрицях координат:

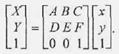
Матричний запис дає можливість наочно описувати декілька перетворень, що йдуть одні за одними. Наприклад, якщо необхідно спочатку виконати перетворення

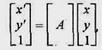
а потім — інше перетворення

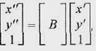
то це можна описати як

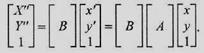
Однак замість двох перетворень можна виконати тільки одне

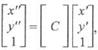
де матриця С дорівнює добутку ВА.

Тепер розглянемо окремі випадки афінного перетворення.

1. Паралельний зсув координат (рис. 2.1).

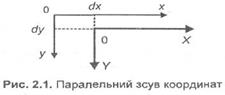
У матричній формі:

Обернене перетворення:

2. Розтягнення-стискання осей координат (рис. 2.2).

Обернене перетворення: