Контрольная работа: Поняття про аберації. Монохроматичні і хроматичні аберації

Величину називають подовжньою сферичною аберацією, а - поперічною сферичною аберацією.

З розгляду рис. 2, а випливає, що якщо площину зображення переміщати вздовж оптичної осі від площини ідеального зображення 2, то можна значно зменшити розмір кола розсіювання. Площина 1, у якій коло розсіювання має мінімальний розмір, називається площиною найкращої установки (ПНУ). При наявності в оптичній системі сферичної аберації тільки третього порядку зсув ПНУ на величину дозволяє отримати , де , – подовжня і поперечна сферичні аберації для променя, що проходить через край вхідної зіниці. На рис. 2, б показаний графік залежності поперечної сферичної аберації від вихідного апертурного кута. Користуючись цим графіком, можна визначити положення ПНУ.

Малюнок 2– Схема для визначення сферичной аберації

Кома . Аберація визначається коефіцієнтом В. З формул (2) маємо

Малюнок 3– Хід променів в оптичній системі при наявності коми

Після переходу до полярних координат і деяких перетворень отримаємо рівняння окружності з радіусом , центр якої зміщений на 2R від точки :

.

Геометричний зміст аберації ілюструє рис. 3. Кома є аберацією широкого похилого пучка променів, яка вносить асиметрію в будівлю пучків.

Астигматизм і кривизна поля . Нехай А = В = Е = 0, С ¹ 0 і D ¹ 0. З формул (2) випливає, що

Переходячи до полярних координат, після перетворення одержуємо рівняння еліпса

,

де а і b- півосі еліпса;, .

Розмір і форма фігури розсіювання змінюються при зміні площини установки. Явище астигматизму полягає в тому, що промені того самого пучка, що йдуть у двох взаємно перпендикулярних площинах (меридіональній та сагитальній), після проходження оптичної системи не збираються в одній точці, а мають різні точки збіжності. Тому у площині, у якій лежить точка збіжності меридіональних променів, еліпс вироджується у відрізок прямої, перпендикулярної до меридіональної площини. У площині, що проходить через точку збіжності сагитальних променів, фігура розсіювання – пряма, що лежить у меридіональній площині. У площині, що лежить посередині між цими площинами, еліпс перетворюється в коло. Положення точок збіжності і меридіональних і сагитальних променів щодо площини ідеального зображення характеризують відрізками і (рис. 4). Різницю називають астигматичною різницею або астигматизмом .

Візьмемо предмет АВ висотою у, розташований у меридіональній площині (рис. 4). Кожній крапці відрізка у відповідатиме меридіональне і сагитальне зображення, наприклад і . З'єднуючи відповідні точки, отримаємо відрізки і , що являють собою меридіональне і сагитальне зображення предмета у. Якщо між кривими і , які являють собою зображення у, провести проміжну (середню) лінію, то отримаємо криву , що характеризує кривизну зображення. При обертанні кривих і навколо оптичної осі отримаємо астигматичні поверхні обертання і поверхню кривизни зображення, дотичні до площини ідеального зображення в точці А' на осі.

Малюнок 4– Поверхонь зображень, утворених астигматичними пучками

Таким чином, якщо коефіцієнти С і D не дорівнюють нулю, то зображення предмета лежить на скривлених поверхнях (параболоїдах), а не на площині.

Дисторсія . Аберація визначається коефіцієнтом Е та координатою у:

.

Дисторсія виявляється у тому, що внаслідок мінливості лінійного збільшення для різних кутів полю порушується подоба зображення предмета. Прямі лінії викривляються, замість правильного квадрата виходять фігури, що зображені на рис. 5. Дисторсія не залежить від координат променя у площині вхідної зіниці, отже, пучок променів, що вийшов з деякої предметної точки, після системи зміститься на відрізок , але його гомоцентричність не порушується і зображення виходить різким.

Малюнок 5– Порушення зображень дисторсією

На практиці у чистому вигляді окремі аберації, а тим більше окремі аберації третього порядку не зустрічаються, тому фігури розсіювання мають складну форму. Крім того, у реальних оптичних системах виявляються й аберації вищих порядків, і фігури розсіювання приймають ще більш складну форму.

Варто зазначити, що число аберацій в залежності від їхнього порядку визначається виразом

,

де N- число аберацій, t- порядок аберацій. Наприклад, якщо t = 3, тo N = 5, при t = 5 N = 9, а якщо t = 7, то N = 14 і т.д. Якість зображення погіршується також внаслідок аберацій, що виявляються при роботі оптичної системи в широкому спектральному діапазоні.

Хроматичні аберації. На відміну від монохроматичних хроматичні аберації виявляються вже в параксіальній області. Параксіальні зображення предмета, які дають оптичні системи у променях з різними довжинами хвиль, розрізняються як по положенню, так і по розмірах в залежності від оптичних характеристик матеріалів, з яких виготовлені оптичні деталі. До основних оптичних характеристик матеріалів (середовищ) відносяться показник заломлення n, середня дисперсія , коефіцієнти дисперсії , відносна приватна дисперсія , де l0- середня довжина хвилі спектрального інтервалу; l1- довжина хвилі, що відповідає короткохвильовій границі спектрального інтервалу; l2- довжина хвилі, що відповідає довгохвильовій границі спектрального інтервалу. Вибір спектрального інтервалу визначається призначенням оптичної системи. Наприклад, для візуальних оптичних приладів, що працюють у видимій області спектра, нм (синьо-блакитна частина спектра), нм (червона частина спектра), (жовта частина спектра).

Характеристики оптичних матеріалів наведені в державних стандартах (див. ДСТ 3514-76, ДСТ 13659-78 і Радянсько-німецький каталог оптичного безбарвного скла).

У параксіальній області розрізняють наступні хроматичні аберації: хроматизм положення, хроматизм збільшення і вторинний спектр. Коротко розглянемо їх.

Хроматизм положення . Ця аберація визначається відстанню між параксіальними зображеннями для двох кольорів l1 і l2, тобто (рис. 6). Виникнення цієї аберації можна пояснити, використовуючи формулу:

.

Через те, що , і , то

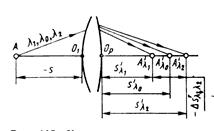Рисунок 6– Хроматизм положення

Для простої тонкої лінзи хроматизм положення визначається співвідношеннями:

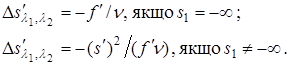(3)

З формул (3) випливає, що для простої тонкої лінзи хроматизм положення виправити неможливо. Найпростішою системою, що дозволяє усунути цю аберацію, є двохлінзовий склеєний об'єктив. Оптичні сили лінз цього об'єктива визначаються зі спільного розв’язання системи двох рівнянь, що задають умову масштабу й умову ахроматизації:

.

Хроматизм положення для системи, яка складена з k нескінченно тонких лінз, обчислюють за формулою:

.

Хроматизм збільшення . Ця аберація визначається відрізком ,що знаходиться як різниця розмірів і зображень для крайніх довжин хвиль l1 і l1, тобто (рис. 7). Хроматизм збільшення виражають у відносній мірі . Для одиночної лінзи хроматизм збільшення може бути обчислений за формулами:

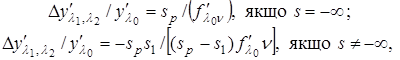
де Sp- положення вхідної зіниці щодо першої поверхні лінзи; S1- положення предмета щодо тієї ж поверхні.

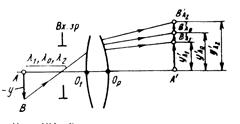Рисунок 7– Хроматизм збільшення

Вторинний спектр . В оптичних системах, які називають ахроматами, параксіальні зображення вісьових точок сполучаються тільки для променів з довжинами хвиль l1 і l2 (рис. 8, крива 1). Залишковий хроматизм за умови називають вторинним спектром.

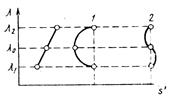Рисунок 8– Графік хроматичної аберації положення

Для тонкого двохлінзового склеєного об’єктива значення вторинного спектра може бути обчислене за формулою

.

Застосування оптичних матеріалів з близькими за значенням відносними частними дисперсіями, але з різними коефіцієнтами дисперсій, наприклад, флюориту, фтористого літію, стекол ОФ4, СТК9 та ін. дозволяє усунути вторинний спектр. Оптичні системи з виправленим вторинним спектром називають апохроматами (рис. 8, крива 2). Апохромати створюють практично незабарвлене зображення.