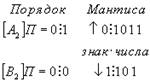Контрольная работа: Порядок выполнения простейших команд гипотетической ЭВМ сложения и умножения
2. Знаковые разряды чисел участвуют в сложении так же, как и значащие.
3. Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
4. При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 2.9. Сложить два числа А10 =7 В10 =16
A2 =+11=+0111;
B2 =+1000=+10000.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
[A2 ]П =[A2 ]OK =[A2 ]ДК =0: 00111;
[B2 ]П =[B2 ]OK =[B2 ]ДК =0: 10000.
Сложение в обратном или дополнительном коде дает один и тот же результат
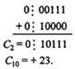
Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.
Пример 2.10. Сложить два числа А10 = + 16 В10 = —7 в ОК и ДК. В соответствии с табл. 2.3 должна быть реализована зависимость А+(-В), в которой второй член преобразуется с учетом знака
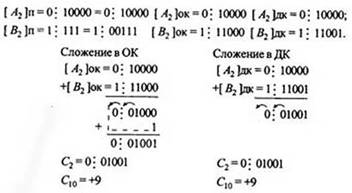
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда. В случае ДК этот перенос игнорируется.
Умножение . Умножение двоичных чисел наиболее просто .реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.
Пример 2.11. Умножить два числа А10 =7 В10 =5.
Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.
Нетрудно видеть, что произведение получается путём сложения частных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение разрядности произведения до n+n=2n. Знак произведения формируется путём сложения знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.
Арифметические операции над двоичными числами с плавающей точкой.
В современных ЭВМ числа с плавающей точкой хранятся в памяти машин, имея мантиссу и порядок (характеристику) в прямом коде и нормализованном виде. Все арифметические действия над этими числами выполняются так же, как это делается с ними, если они представлены в полулогарифмической форме (мантисса и десятичный порядок) в десятичной системе счисления. Порядки и мантиссы обрабатываются раздельно.
Сложение (вычитание). Операция сложения (вычитания) производится в следующей последовательности.
1. Сравниваются порядки (характеристики) исходных чисел путем их вычитания р=р1-р2. При выполнении этой операции определяется, одинаковый ли порядок имеют исходные слагаемые.
2. Если разность порядков равна нулю, то это значит, что одноименные разряды мантисс имеют одинаковые веса (двоичный порядок). В противном случае должно проводиться выравнивание порядков.
3. Для выравнивания порядков число с меньшим порядком сдвигается вправо на разницу порядков Ар. Младшие выталкиваемые разряды при этом теряются.
4. После выравнивания порядков мантиссы чисел можно складывать (вычитать) в зависимости от требуемой операции. Операция вычитания заменяется операцией сложения в соответствии с данными табл. 2.3. Действия над слагаемыми производятся в ОК или ДК по общим правилам.
5. Порядок результата берется равным большему порядку.
6. Если мантисса результата не нормализована, то осуществляются нормализация и коррекция значений порядка.
Пример 2.13. Сложить два числа А10 =+1.375; B10 =-0.625.
А2 =+1.011=0: 1011*101 ; B2 =-0.101=-0:101*100 .
В нормализованном виде эти числа будут иметь вид: