Контрольная работа: Построение годографов Михайлова при помощи пакета MATHCAD

где с – соответствующий постоянный коэффициент при определённом порядке частоты .

Применяя (15) к нашей задаче, получим:

(16)

а также

(17)

Имея данные в виде (16) и (17), приступим к вышеупомянутому алгоритму построения годографа Михайлова с помощью «MathCad».

Шаг 1. Зададим диапазон индекса i:

(18)

Шаг 2. Определим исследуемый диапазон и шаг частоты (примем с частотным шагом 0,1):

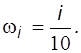(19)

Шаг 3. Введём вещественную (16) и мнимую (17) части характеристического уравнения:

(20)

и

(21)

Шаг 4. При выполнении вычислений (19), (20) и (21), формируются массивы значений частоты , вещественной и мнимой частей (рис. 7).

Шаг 5. Имея рассчитанные массивы значений и , подобно предыдущему примеру, построим частотную функцию Михайлова. После определения параметров графика, получим годограф, приведенный на рис. 8.

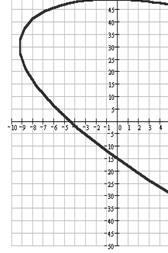
Рисунок 7 – Массивы значений , и , рассчитанные в «MathCad»

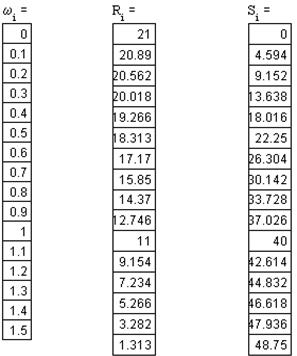
Рисунок 8 – Годограф Михайлова для САУ позиционированием НСУ

На основе анализа полученных данных, можно сделать вывод, что построенный годограф Михайлова, начинаясь на вещественной положительной оси, огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.

Что же касается анализа последних публикаций [2] и сравнения с лучшими аналогами [3], то необходимо отметить факт отсутствия подобной функции (построение годографа Михайлова) в пакете «MATLAB» [1, 4], который, обычно, используется для моделирования различных САУ, что, собственно, и послужило главной причиной создания данного алгоритма.

Перспективы развития данной работы заключаются в создании универсального инструмента для анализа комплексной частотной функции Михайлова, способного выполнить все вычисления уже на этапе задания характеристического уравнения, тем самым полностью автоматизируя этот процесс.

Таким образом, для достижения цели, в ходе написания исследования, была решена главная проблема – получение простого и наглядного инструмента для решения задач расчёта устойчивости САУ, что является обязательным условием работоспособности любого промышленного робота и манипулятора. Также были выполнены следующие задачи: сформирован алгоритм построения комплексной частотной функции Михайлова при помощи математического пакета «MathCad», выполнен анализ устойчивости САУ МПР по данному критерию, кроме того, – приведены практические примеры реализации данного алгоритма.

Список использованной литературы

1. Дорф Р. Современные системы управления / Р. Дорф, Р. Бишоп. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.

2. Юревич Е.И. Основы робототехники 2-е издание / Е.И. Юревич. – С-Пб.: БХВ-Петербург, 2005. – 416 с.

3. Yim Y. Modular Robots / Y. Yim, Y. Zhang, D. Daff // IEEE SPECTRUM. – 2002. – # 2. – P. 30 – 34.

4. Олссон Г. Цифровые системы автоматизации и управления / Г. Олссон, Дж. Пиани. – С-Пб.: Невский Диалект, 2001. – 557 с.