Контрольная работа: Пределы Сравнение бесконечно малых величин
.
В нашем случае
.
Из полученного выражения следует, что с увеличением 
величина 
растет. Действительно, перейдем от к 
. Это приведет к тому, что число слагаемых возрастет на одно. Кроме того, величина множителей, заключенных в скобки, тоже возрастет, так как 
. Но если увеличивается число слагаемых и сами слагаемые растут, то 
. Значит, числовая последовательность 
монотонно возрастает.
Докажем теперь, что данная последовательность ограничена сверху. Заменим все скобки вида 
единицей. Так как 
, то
.
Кроме того 
, 
,..., 
. Значит,
.
В правой части неравенства после цифры 2 стоит убывающая геометрическая прогрессия. Как известно, сумма первых членов такой прогрессии равна: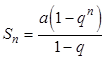 
. В нашем случае 
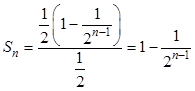. С ростом величина 
будет, очевидно, стремится к единице. Значит, 
, то есть, ограничено сверху.
Итак, мы получили, что 
. Но так как монотонно возрастающая последовательность ограниченная сверху, то она имеет предел:
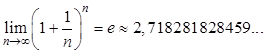
Можно доказать, что данный предел справедлив не только для натуральных чисел, но и для любых значений 
:
.
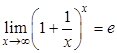Полученное выражение и называется вторым замечательным пределом.
Число 
используется для введения натуральных логарифмов. Такие логарифмы обозначаются 
, при этом 
.
Следствие 3.1.
.
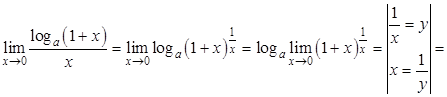
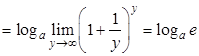В частности, если 
, то 
.
Следствие 3.2 .
.
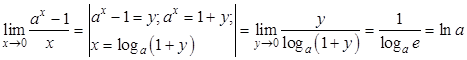В частности, если , то 
.
4. Сравнение бесконечно малых величин
Как следует из определения бесконечно малых величин, все они стремятся к нулю, но скорость этого стремления может быть различна. Поэтому все бесконечно малые величины можно сравнивать между собой.
Пусть даны две бесконечно малые величины 
и 
при 
, то есть 
, 
.
Определение 4.1 . Функции и называются бесконечно малыми величинами одного порядка малости, если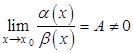 
.
Определение 4.4. Функция называется бесконечно малой величиной более высокого порядка малости, чем , если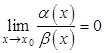 
.
Определение 4.3 . Функция называется бесконечно малой величиной более низкого порядка малости, чем , если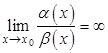 
.
Тот факт, что , например, имеет более высокий порядок малости, чем , можно обозначить следующим образом: 
.