Контрольная работа: Представление о логике мышления и познания философов XIX – начала XX вв.
От чистой математики Рассел отличает прикладную математику, которая состоит в применении формальных выводов к материальным данным.
Для того чтобы показать, что чистая математика сводится к логике, Рассел берет систему аксиом арифметики, сформулированную Пеано, и пытается их логически доказать, а три неопределяемых у Пеано понятия: "нуль", "число", "следующее за" - определить в терминах своей логической системы. Все натуральные числа Рассел также считает возможным выразить в терминах логики, а следовательно, свести арифметику к логике. А так как, по его мнению, вся чистая математика может быть сведена к арифметике, то и математика может быть сведена к логике. Рассел пишет: "Логика стала математической, математика логической. Вследствие этого сегодня совершенно невозможно провести границу между ними. В сущности это одно и то же. Они различаются как мальчик и мужчина; логика - это юность математики, а математика - это зрелость логики"". Рассел считает, что не существует пункта, где можно было бы провести резкую границу, по одну сторону которой находилась бы логика, а по другую - математика.
Но в действительности математика несводима к логике. Предметы изучения этих наук различны. Нами ранее были указаны характерные черты, присущие логике как науке. У математики другие задачи и функции.
В большом трехтомном труде "PrincipiaMathematica" есть две стороны. Первая - заставляющая видеть в нем один из основных истоков современной математической логики. Все, что связано с этой стороной PrincipiaMathematica, получило в дальнейшем такое развитие в математической логике, которое сделало эту новую область науки особенно важной для решения не только труднейших задач теоретической математики и ее обоснования, но и целого ряда весьма важных для практики задач вычислительной математики и техники.
Другая сторона этого произведения - точнее, даже не самого этого произведения, а философских "обобщений", делаемых логицистами со ссылкой на него, - принадлежит уже к области попыток использовать его для "доказательства" положения, что математика-де сводится к логике. Именно эта сторона и относится к области неправильных выводов. Именно ее и опровергает дальнейшее развитие науки, которое обнаружило, что эта попытка Рассела не удалась. И это не случайно. Дело не в том, что Рассел в каком-то смысле не совсем удачно построил свою систему. Дело в том, что и нельзя построить формальную "логическую систему" с точно перечисленными и эффективно выполнимыми правилами вывода, в которой можно было бы формализовать всю содержательную арифметику. Это обстоятельство представляет собой содержание известной теоремы австрийского математика и логика К. Гёделя о неполноте формализованной арифметики, из которой следует непосредственно, что определение математических понятий в терминах "логики" хотя и обнаруживает некоторые связи этих понятий с логикой, но не лишает их тем не менее специфически математического содержания. Формализованная система имеет смысл лишь при наличии содержательной научной теории, систематизации которой данная формализованная система должна служить.
Однако Г. Фреге и Б. Рассел пришли в логическом анализе к ряду интересных результатов, относящихся к понятиям "предмет", "имя", "значение", "смысл", "функция", "отношение" и др. Особо следует подчеркнуть важность разработанной Расселом теории типов (простой и разветвленной), цель которой состоит в том, чтобы помочь разрешить парадоксы в теории множеств. Рациональное зерно разветвленной теории типов Рассела состоит в том, что она является конструктивной теорией.
4. Дать ответ на тестовое задание
Отношение, которое существует между двумя понятиями, объем которых только частично входит друг в друга:
а) отношение противоположности (контрастности);
б) отношение соподчинения;
в) отношение пересечения;
г) отношение подчинения.
Правильный ответ - в).
В отношении пересечения (перекрещивания) находятся понятия, объем одного из которых частично входит в объем другого понятия. Содержание этих понятий различно.
В отношении пересечения находятся понятия "юрист" (А) и "депутат Верховного Совета" (В): некоторые юристы являются депутатами Верховного Совета (как некоторые депутаты Верховного Совета - юристами).
С помощью круговых схем это отношение изображается в виде двух пересекающихся кругов (рис.2).
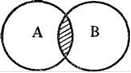
Рис.2.
А - юрист
В - депутат Верховного Совета
В совместившейся части кругов А и В (заштрихованная часть кругов) мыслятся те юристы, которые являются депутатами Верховного Совета, в несовместившейся части круга А - юристы, не являющиеся депутатами Верховного Совета, в несовместившейся части крута В - депутаты Верховного Совета - не юристы.
Понятия, находящиеся в отношении пересечения, называются пересекающимися (перекрещивающимися).
Литература
1. Иванов Е.А. Логика. - М., 1996.
2. Краткий словарь по логике / Д.П. Горский, А.А. Ивин, А.Л. Никифоров; Под ред. Д.П. Горского. - М.: Просвещение, 1991.
3. Кириллов В.И., Старченко А.А. Логика: Учебник. - М.: Высш. школа, 1982.
4. Івін О.А. Логіка. - К., 1996.
5. О.М. Бандурка, О.В. Тягло. Курс логіки. - Київ, 2002.
6. Тофтул Л.Г. Логіка. Посібник для студентів ВНЗ. - Київ, 1999.
7. В. Є. Жеребкін. Логіка. - Київ, 2001.
8. Ивин А.А. Никифоров А.Д. Словарь по логике. - М., 1998.