Контрольная работа: Прикладне вживання методів дискретної математики

c) SÄT= {{b, c}, {b, e}, {b, f}, {b, i}, {c, c}, {c, e}, {c, f}, {c, i}, {e, c}, {e, e}, {e, f}, {e, i}, {i, c}, {i, e}, {i, f}, {i, i}}.

2.

a) h³ =

у	x1	x2	x 3
2	b	e	6
3	с	e	5
5	с	b	2
4	а	e	5
3	с	e	6
4	а	c	5

b) h⁴ =

c) h⁵ =

у	x1	x2	x 3
3	с	e	5
4	а	e	5

d) h⁶ =

у x1 x2 x 3 2 b e 6 5 с b 2

3.

a)

r 3	x1	x2	x3	x4
x1	1	1	0	1
x2	1	1	0	1
x3	1	1	1	0
x4	0	1	1	1

b)

r 4	x1	x2	x3	x4
x1	1	1	0	1
x2	0	1	0	0
x3	0	0	0	0
x4	0	0	1	1

c)

r 3	x1	x2	x3	x4
x1	0	0	0	0
x2	0	0	0	1
x3	1	0	1	0
x4	0	1	0	0

d)

r 3	x1	x2	x3	x4
x1	0	0	0	0
x2	1	0	0	1
x3	1	1	1	0
x4	0	1	0	0

2. Задача 2

У колоді 52 карти. У скількох випадках при виборі з колоди 10 карт серед них виявляться: а) рівно один туз; б) хоча б один туз; в) не менше двох тузів; г) рівно два тузи?

Відповідь:

а) Всього у колоді 4 тузи. Отже за правилом добутку перемножимо ймовірність вибору з чотирьох тузів одного туза та ймовірність вибору інших карт, тобто 9 з 48:

.

б) Хоча б один туз – це означає може бути і 4, і 3, і 2, і 1. Отже для розв'язку необхідно від ймовірності вибору 10 карт з 52 відняти ймовірність вибору 10 карт з 48:

.

в) Не менше двох тузів – означає, що з 10 карт буде 4, 3 або 2 тузи. Рішенням буде попередня відповідь від якої відняти ймовірність вибору 1 туза (першої відповіді):

.

г) Аналогічно розв'язку першого завдання отримаєм:

3. Задача 3

Граф заданий матрицею вагів. Побудувати для нього остов мінімальної ваги використовуючи алгоритми Пріма та Краскала, за алгоритмом Флойда обчислити найкоротші шляхи графа.

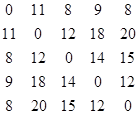
Відповідь:

Будова графа:

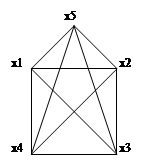
Побудова остову мінімальної ваги по алгоритму Краскала:

Встановлюємо частковий порядок по вазі ребер графа:

L13	L15	L14	L12	L23	L45	L34	L35	L24	L25
8	8	9	11	12	12	14	15	18	20