Контрольная работа: Прикладне вживання методів дискретної математики
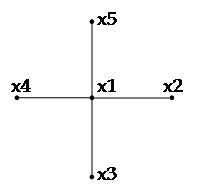
| Крок | Ребра остову | Вершини остову | |||||||
| L13 | L15 | L14 | L12 | x1 | x2 | x3 | x4 | x5 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Lij | 8 | 8 | 9 | 11 | L=8+8+9+11=36 | ||||
Обчислення найкоротших шляхів за алгоритмом Флойда:
Будуємо матрицю вагів та матрицю переходів:
А0 = 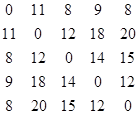 Р0 =
Р0 = 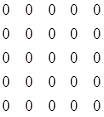
Елементи матриці вагів будемо знаходити за формулою:
Ak [i; j] = min (Ak-1 [i; j], Ak-1 [i; k] + Ak-1 [k; j])
Перша ітерація:k=1
А1 = 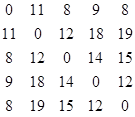 Р1 =
Р1 = 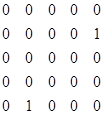
Друга ітерація:k=2
А2 = 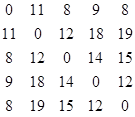 Р2 =
Р2 = 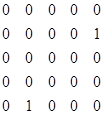
Третя ітерація:k=3
А3 = 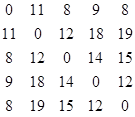 Р3 =
Р3 = 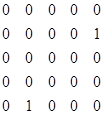
Четверта ітерація:k=4
А4 = 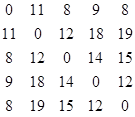 Р4 =
Р4 = 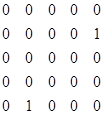
П’ята ітерація:k=5
А5 = 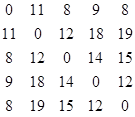 Р5 =
Р5 = 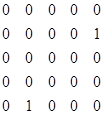
4. Задача 4
Знайти мінімальну ДНФ логічної функції F= F(хг , х2 , х3 , х4 ), яка дорівнює одиниці на наборах 2, 3, 4, 11, 14, 15 і нулю на решті наборів.
Відповідь:
Спочатку необхідно подати функцію у ДДНФ.
ДДНФ =x1 x2 x3 x4 Úx1 x2 x3 x4 Úx1 x2 x3 x4 Úx1 x2 x3 x4 Úx1 x2 x3 x4 Úx1 x2 x3 x4
Виконуємо склеювання:
1-2 x1 x2 x3
1-4 x2 x3 x4
2-4 x2 x3 x4
4-6 x1 x3 x4
5-6 x1 x2 x3
ДДНФ = x1 x2 x3 Úx2 x3 x4 Úx2 x3 x4 Úx1 x3 x4 Úx1 x2 x3 Úx1 x2 x3 x4
1-2 x2 x3