Контрольная работа: Проектирование автотранспортных предприятий
Указанных ошибок можно избежать, если применять расчёты, при которых в качестве исходных данных принимаются во внимание не детерминированные, а случайные величины и законы их распределения. В отличие от детерминированных такие расчёты называются расчётами с применением вероятностных методов, или вероятностными (стохастическими) методами расчёта.
Детерминированные методы определения потребности в капитальных ремонтах автомобилей могут приводить к ошибкам в три и более раз. Кроме того, рассмотренный выше пример показывает, что при определении потребности в ремонтах, помимо годового пробега и межремонтных периодов, необходимо принимать во внимание распределение сроков службы или пробега автомобиля с начала эксплуатации, т.е. возраст автомобилей.
При расчётах необходимо также учитывать рассеивание межремонтных периодов.
2. Вероятностный метод расчёта
Для того чтобы правильно определить потребность в капитальных ремонтах автомобилей, недостаточно принимать во внимание только их количество, годовой пробег в среднем на один автомобиль и среднее значение межремонтного периода, как это предусматривается классической формулой (2.1). Для получения правильного ответа необходимо также учитывать законы распределения:
1) автомобилей по пробегу с начала эксплуатации в начале планируемого периода, например года;
2) годовых пробегов автомобилей.
Если в начале года автомобили КАЗ-608 имели пробег с начала эксплуатации 50 тыс. км и в течение года пройдут ещё по 50 тыс. км. Итого 50 + 50 = 100 тыс. км с начала эксплуатации. Это не значит, что все 100 % автомобилей в течение года потребуют капитального ремонта, как это имело бы место при детерминированном расчёте. Если величина межремонтного периода не детерминирована, а распределяется по нормальному закону распределения, то межремонтные периоды не равны точно 100 тыс. км для всех автомобилей, а распределяются в интервале 75…225 тыс. км. При этом благодаря симметрии нормального закона распределения количество автомобилей с межремонтным периодом 75…150 тыс. км составляет 50 % и с периодом 150…225 тыс. км – также 50 %. Если с начала эксплуатации к концу года все автомобили пройдут по 100 тыс. км, то только половина из них, для которых межремонтный период меньше или равен 100 тыс. км потребует капитального ремонта, а вторая половина не потребует. Чтобы получить правильный ответ, необходимо знать не только среднее значение межремонтного периода, но и закон распределения межремонтных периодов отдельных автомобилей парка.
Таким образом, годовой пробег автомобиля lг и межремонтный период lк являются случайными величинами. Опытные данные показывают, что обе эти величины распределяются по законам, весьма близким к нормальному закону распределения. Основные параметры законов распределения этих величин: их средние значения (математическое ожидание) - lг и lк ; средние квадратичные отклонения – σг и σк , которые, согласно опытным данным, могут быть определены по формулам:
σг ≡ (0,2…0,25) * lг , (2.2)
σг ≡ 0,23 * 40 = 9.2,
σк ≡ (0,2…0,25) * lк , (2.3)
σк ≡ 0,18 * 280 = 50.4
В отношении распределения автомобилей по пробегу с начала эксплуатации l0 в результате обработки статистического материала не удалось выявить какой-либо определённой закономерности. Поэтому распределение автомобилей по величине пробега l0 в каждом автопредприятии может существенно отличаться от распределения для других парков и часто не подчиняется ни нормальному, ни какому-либо другому из известных законов распределения. Распределение автомобилей в парке по пробегу с начала эксплуатации принято задавать статистическим рядом. При этом весь диапазон пробега с начала эксплуатации разделяется на разряды распределения и в каждом разряде указывается количество автомобилей, имеющих соответствующий пробег.
Действующим положением о техническом обслуживании и ремонте подвижного состава автомобильного транспорта предусмотрены следующие разряды распределения автомобилей по пробегу с начала эксплуатации: от 0 до 0,25 lк , от 0,25 до 0,50 lк и т.д. через каждые 0,25 lк . При этом статистический ряд распределения будет выглядеть так.
Таблица 2.1. Статистический ряд распределения автомобилей по пробегу от начала эксплуатации.
| № разряда | Диапазон разряда Wi | Среднее значение пробега в разряде l0 | Количество автомобилей в разряде Ан |
| 1 | 0…70 | 35 lк | 20Н1 |
| 2 | 70…140 | 105 lк | 60Н1 |
| 3 | 140…210 | 175 lк | 100Н1 |
| 4 | 210…280 | 245 lк | 50Н1 |
| 5 | 280…350 | 315 lк | 50Н1 |
Стохастическими методами расчёта годовая потребность в капитальных ремонтах Nк , шт. определяется по формуле:
Nк =![]() н
н 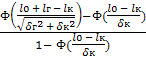 (2.4)
(2.4)
где n – число разрядов распределения автомобилей в парке по пробегу с начала эксплуатации;
i – порядковый номер разряда распределения автомобилей в парке по пробегу с начала эксплуатации;
Ан – списочное количество автомобилей в i-м разряде распределения (350) шт;
Ф – функция Лапласа, значения которой определяются по (приложение А.1);
l0 –математическое ожидание (среднее значение) пробега автомобилей с начала эксплуатации в разряде распределения, тыс. км
lг – математическое ожидание годового пробега автомобилей 40 тыс. км;
lк – математическое ожидание пробега автомобилей до капитального ремонта 280 тыс. км;
σг – среднее квадратичное отклонение годового пробега автомобилей 9.2 тыс. км;
σк – среднее квадратичное отклонение пробега автомобилей до капитального ремонта 50.4 тыс. км.
При практическом использовании формулы (2.4) следует иметь в виду следующее правило знаков:
Ф(-х) = - Ф(х)