Контрольная работа: Процент. Наращение
В случае приведения по вкладу Р для нахождения дисконтированных значений достаточно воспользоваться формулами (1) и (2), решив их относительно величины Р.
В результате получим две формулы:
![]() (3)
(3)
при дисконтировании по простым процентам и
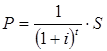 (4)
(4)
для сложных процентов. Стоящие в этих формулах мультипликаторы
![]() и
и ![]()
показывают, какую долю составляет Р в величине S при простой и соответственно сложной ставке процентов и называются дисконтными множителями.
Величину Р, найденную дисконтированием S по вкладу, называют современной, или приведенной величиной S. Это понятие является одним из важнейших в количественном анализе финансовых операций, поскольку именно с помощью дисконтирования учитывается такой фактор, как время.
Формулы дисконтирования по платежу (второй подход) можно получить, используя формулы (1) и (2) с заменой схемы начисления процентов на вклад Р схемой их удержания с суммы S за тот же срок вложения. За основу их построения принять понятие единичного периода удержания процентов (дисконтирования) и учетной ставки d, которая фиксирует процентное или долевое уменьшение суммы S на один период «назад». Отсюда следует, что на начало этого периода эквивалентная выплате S сумма составит величину Р, которая при дробном измерении ставки определяется формулой P=S-d·S.
По отношению к следующим периодам учетная ставка трактуется поразному в зависимости от принятой схемы дисконтирования: по простым или по сложным процентам. В первом случае удержания денежных сумм (дисконты) по каждому периоду будут составлять все тот же процент d от все той же суммы S. В результате такого дисконтирования за t периодов получиться величина
Pt =S - tdS=S(1 - td)(5)
В отличие от этого при учете по сложной ставке последовательные по периодам снижения берутся как один и тот же процент d, но не от одной и той же величины S, а каждый раз от новой, полученной в результате дисконтирования на соседний период. Отсюда следует формула дисконтирования (учета) по сложным процентам, где в качестве процента выступает доля удержания d:
Pt =S·(1 - d)t .
(6)
Схема дисконтирования (3) и (4) широко применяется в многообразных задачах финансового анализа, в том числе для сравнения потоков платежей и при расчете стоимости облигаций и прочих ценных бумаг.
Дисконтирование по удержанию (5) и (6) используется при учете векселей. Суть этой финансовой операции состоит в следующем. Некто выдает вексель (расписку) с обязательством уплатить сумму S на определенную дату T. Владелец векселя в случае нужды может досрочно учесть его, т.е. получить деньги раньше срока в коммерческом банке (КБ) по установленной последним учетной ставке d, которая уменьшает сумму выплаты. В зависимости от принятых условий учет проводиться по простым (5) или сложным (6) процентам.
Такой вексель, который допускает участие третьих лиц, называется переводным или траттой. В дальнейшем на дату Т, банк предъявляет вексель тому, кто его выписал, и получает сумм S, извлекая из этой операции собственную выгоду: учитывал по меньшей сумме, а получил большую.
Пример. Тратта выдана на сумму 100 тыс.грн. с уплатой 17.11. Владелец документа учел его в банке 23.09 по учетной ставке 8%. Так как до погашения обязательства период равен 55 дням, то полученная сумма (без уплаты комиссионных) составит
![]() грн.
грн.
а дисконт равен D=100000-98777,78=1222,22 грн.
Задание
1) Найти 41,5%от заданного числа 905.
2) Найти, сколько процентов составляет число 32,7 от заданного числа 79,39
3) Найти число q, если данное число 15 составляет 1,98% от него.
4) Найти наращенную сумму Sn по вкладу 854 при ставке 7,3% для случая простых и сложных процентов за 3мес. периодов.
5) Найти дисконт d при тратте 1203 и учетной ставке 9%, а также годовую доходность операции учета по простой ставке для банка, если известны сроки уплаты: 1.10 и учета документа: 15.7.
Решение
1) Найти 41,5% от числа 905?