Контрольная работа: Проверка гипотезы о законе распределения случайной величины по критерию Пирсона

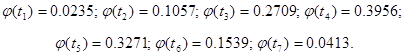
. (7)

Полученные значения занесем в таблицу 4

Таблица 4

21.5	0.0025
28.5	0.0114
35.5	0.0291
42.5	0.0425
49.5	0.0351
56.5	0.0165
63.5	0.0044

3. Критерий согласия 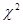(Пирсона)

Найду соответствующие вероятности для каждого разряда

Из ТВ для нормальной случайной величины

(8)

Значения функции Лапласа, находим в приложении 2, учебника Вентцель Е.С., Овчаров Л.А., теория вероятностей и её инженерные приложения. Учеб. пособие для вузов. - 2-е изд., стер. - М.: Высш. шк., 2000.

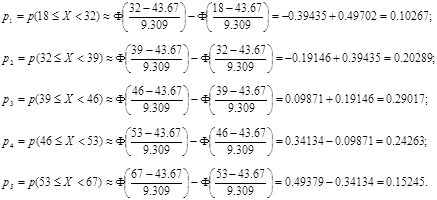
Таблица 5

	7	10	20	13	10
	0,12567	0, 20289	0,29017	0,24263	0,15245
	7,5402	12,1734	17,4102	14,5578	9,1470
	-0,5402	-2,1734	2,5898	-1,5578	0,8530
	0,2918	4,7237	6,7071	2,4267	0,7276
	0,0387	0,3880	0,3852	0,1667	0,079

. (9)

- расчетное

Найдем число степеней свобод

(10)

Где k=5; s=3;

r=2

Для

Получили:

.

Гипотеза о нормальном распределении генеральной совокупности, из которой сформирована выборка, не противоречит экспериментальным данным.

4. Нахождение доверительного интервала

4.1 Оценка математического ожидания

4.2 Оценка дисперсии .

4.3 Среднеквадратичное отклонение оценки

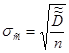, (11)

.

4.4 По функции Лапласа, определим t

;