Контрольная работа: Проверка гипотезы о законе распределения случайной величины по критерию Пирсона
Под случайной выборкой объема n понимают совокупность случайных величин ![]() , не зависимых между собой. Случайная выборка есть математическая модель проводимых в одинаковых условиях независимых измерений.
, не зависимых между собой. Случайная выборка есть математическая модель проводимых в одинаковых условиях независимых измерений.
Таблица 1
| 42,7; | 37,6; | 45,1; | 55,4; | 50,7; | 30,7; | 31,9; | 43,8; |
| 47,5; | 42,1; | 57,7; | 21,3; | 45,5; | 45,3; | 46,2; | 50,9; |
| 33,2; | 40,4; | 40,0; | 59,6; | 46,0; | 44,0; | 37,0; | 44,7; |
| 64,6; | 58,9; | 31,3; | 59,2; | 45,5; | 53,3; | 43,6; | 37,5; |
| 33,0; | 42,6; | 39,6; | 51,5; | 47,4; | 48,6; | 33,8; | 29,2; |
| 33,7; | 48,5; | 44,4; | 37,6; | 45,1; | 36,0; | 26,4; | 38,0; |
| 49,7; | 52,1; | 42,7; | 49,0; | 31,9; | 52,2; | 60,6; | 44,6; |
| 43,9; | 59,4; | 53,7; | 45,9. |
2. Упорядоченная выборка
Упорядоченной статистической совокупностью будем называть случайную выборку величины в которой расположены в порядке возрастания ![]()
Таблица 2
| 21,3; | 26,4; | 29,2; | 30,7; | 31,3; | 31,9 | 31,9; | 33,0; |
| 33,2; | 33,7; | 33,8; | 36,0; | 37,0; | 37,5 | 37,6; | 37,6; |
| 38,0; | 39,6; | 40,0; | 40,4; | 42,1; | 42,6 | 42,7; | 42,7; |
| 43,6; | 43,8; | 43,9; | 44,0; | 44,4; | 44,6 | 44,7; | 45,1; |
| 45,1; | 45,3; | 45,5; | 45,5; | 45,9; | 46,0 | 46,2; | 47,4; |
| 47,5; | 48,5; | 48,6; | 49,0; | 49,7; | 50,7 | 50,9; | 51,5; |
| 52,1; | 52,2; | 53,3; | 53,7; | 55,4; | 57,7 | 58,9; | 59,2; |
| 59,4; | 59,6; | 60,6; | 64,6. |
![]() .
.
Определим шаг или длину интервала, по формуле Стерджесса
![]() , (1)
, (1)
![]() .
.
Таблица 3
| [18; 25) | 21,5 | 1 | 0,0167 | 0,0024 |
| [25; 32) | 28,5 | 6 | 0,1 | 0,0142 |
| [32; 39) | 35,5 | 10 | 0,1667 | 0,0238 |
| [39; 46) | 42,5 | 20 | 0,3333 | 0,0476 |
| [46; 53) | 49,5 | 13 | 0,2167 | 0,0309 |
| [53; 60) | 56,5 | 8 | 0,1333 | 0,0190 |
| [60; 67) | 63,5 | 2 | 0,0333 | 0,0048 |
| 60 | 1 |
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() - частота;
- частота;
![]() - относительная частота;
- относительная частота;
![]() - плотности относительных частот.
- плотности относительных частот.

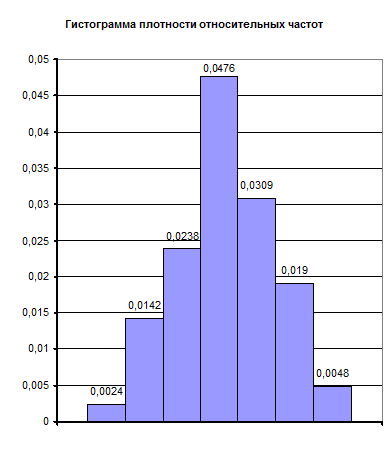
Рис. 1. Гистограмма плотности относительных частот
По построенной гистограмме (рис.1) можно предположить, что данное распределение подчиняется нормальному закону. Для подтверждения выдвинутой гипотезы проведем оценку неизвестных параметров, для мат. Ожидания
![]() , (2)
, (2)
![]() .
.
для несмещенной оценки дисперсии
![]() , (3)
, (3)
![]()
Функция плотности имеет вид
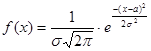 , (4)
, (4)
где ![]() ,
,
![]() .
.
Пользуясь приложением 3 в учебнике Вентцель Е.С. - "Теория вероятностей" - М.: Высшая школа, 1998., получим значения ![]()
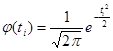 (5)
(5)
--> ЧИТАТЬ ПОЛНОСТЬЮ <--