Контрольная работа: Расчет мощности двигателя
для шестерни [σH1] = (2HB1 +70)* KHL / [SH] = (2*230+70)*1 / 1.1 =482 МПа;
для колеса [σH2] = (2HB2 +70)* KHL / [SH] =(2*200+70)*1 / 1.1 = 428МПа.
Тогда расчетное допускаемое контактное напряжение [σH] = 0,45 (482 + 428) = 410 МПа. Требуемое условие [σH] < 1,23 [σH2] выполнено.
Коэффициент KHβ, несмотря на симметричное расположение колес относительно опор, примем выше рекомендуемого для этого случая, так как со стороны цепной передачи действуют силы, вызывающие дополнительную деформацию ведомого вала и ухудшающие контакт зубьев. Принимаем предварительно по табл. 3.1, как в случае несимметричного расположения колес, значение KHβ = 1,25.
Принимаем для косозубых колес коэффициент ширины венца по межосевому расстоянию ψba = b /aω = 0,4.
Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев по формуле
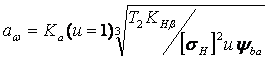 =
=
=43 (5+1)![]() мм.
мм.
где для косозубых колес Ка = 43, а передаточное число нашего редуктора u = 5.
Ближайшее значение межосевого расстояния по ГОСТ 2185–81 aw = 200 мм.
Нормальный модуль зацепления принимаем по следующей рекомендации: mп = (0,01 – 0,02) aw = (0,01 – 0,02) 200 = 2 – 4 мм; принимаем по ГОСТ 9563 – 80 mn = 2,5 мм.
Примем предварительно угол наклона зубьев β = 10° и определим числа зубьев шестерни и колеса:
![]() =(400+0,985)/15=26,2
=(400+0,985)/15=26,2
Принимаем z1 = 26; тогда z2 = z1u =26*5 = 130.
Уточненное значение угла наклона зубьев![]()
β = 12°50'.
Основные размеры шестерни и колеса:
диаметры делительные:
d1=mn z1 / cosβ = 2.5 *26/ 0.975 = 66.66 мм;
d2=mn z2 / cosβ = 2.5*130 / 0.975 = 333.34 мм;
Проверка: aω = 0.5 (d1 + d2) = 0.5 (66.66+333.34) = 200 мм.
диаметры вершин зубьев:
da1 = d1 + 2mn = 66,66 + 2*2,5 = 71,66 мм;
da2 = d2 + 2mп = 333,34 + 2*2,5 = 338,34 мм;
ширина колеса b2 = Ψba *aω = 0,4*200 = 80 мм;
ширина шестерни b1 = b2 + 5 мм = 85 мм.
Определяем коэффициент ширины шестерни по диаметру:
Ψbd = b1 / d1 = 85 / 66,66 = 1,275.
Окружная скорость колес и степень точности передачи v = 0,5 ω1d1 =101,5*66,66 / = 3.38 м/с.