Контрольная работа: Расчеты гидравлических величин

Рассчитаем площадь вертикальной поверхности проекции АВС:

S_x =d·2 R =4·2·0,6=4,8 (м³ )

Из условия – сосуд находится под избыточным давлением Р_м = 7000 Па это давление и будет давлением на свободной поверхности жидкости в сосуде Р₀ т.е. Р_м = Р₀ .

Рассчитаем усилие F₁ необходимое для удержания крышки:

F₁ = ρ₁ g h_c S_x + P ₀ S_x = 790·9,81·11,5·4,8 + 7000·4,8 = 427794,48 + 33600 =

=461394,48 (Н)

Рассчитаем усилие F₂ необходимое для удержания крышки:

F₂ = 772,99·9,81·11,5·4,8 + 7000·4,8 = 418583,36 + 33600 = 452183,36 (Н)

Построим эпюру гидростатического давления жидкости на стенку, к которой прикреплена крышка:

Р_Н = ρgН + P ₀ = 790·9,81·11,5 + 7000= 89033 + 7000=96033 (Па)

Вертикальная составляющая силы давления равна весу жидкости в объеме тела давления:

V = π R ² d /2 =(3,14·0,6² ·4)/2=2,26 (м³ )

F_y = G = ρ · g · V =790·9,81·2,26=17514,8 (Па)

Р0

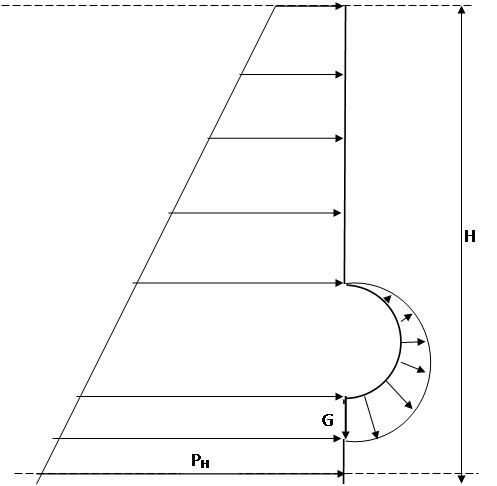
Эпюра гидростатического давления

Задача №2

Определить расход жидкости вытекающей через насадок из резервуара, в котором поддерживается постоянный уровень жидкости Н . Диаметр насадка d .

Построить эпюру давления на стенку, в которой расположен насадок.

Определить длину насадка.

Исходные данные Рисунок

Н	α	d	h
м	0	м	м
14	6	0.03	8

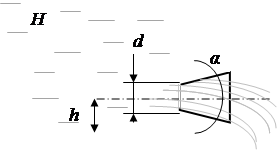
Решение

Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:

Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ .

Так как жидкость вытекает из резервуара через конический расходящийся насадок то ε=1 , а μ = φ .

Так как насадок конический расходящийся с углом 6⁰ , то значение коэффициента истечения выбираем φ = μ = 0,45

Так как профиль отверстия истечения жидкости представляет собой круг, то его площадь вычисляется по формуле: