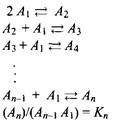Контрольная работа: Разнообразие систем, формируемых дифильными веществами

4. Модель фазового разделения

В этой модели образование мицелл рассматривается как процесс, аналогичный фазовому разделению, причем мицеллы являются новой фазой, а KKM — концентрацией насыщения раствора молекулярным ПАВ. Избыток ПАВ сверх ККМ, следовательно, влияет только на концентрацию мицелл. Эта модель мицеллообразования особенно удобна для интерпретации экспериментальных данных. В результате физико-химических измерений получают среднюю величину по различным состояниям, в которых могут находится молекулы ПАВ. Ниже KKM существуют только отдельные молекулы ПАВ, и среднее значение величины Q равно

Для концентраций выше ККМ, учитывая, что C_m i_c = C_tot - KKM и C_aq = ККМ, получим:

Для концентраций существенно выше KKM <Q> приближается к Qmc· Модель фазового разделения не вызывает трудностей при ее использовании, она наглядна и подходит для описания многих систем. Она выполняется тем

лучше, чем выше числа агрегации ПАВ в мицеллах.

4.1 Модель, основанная на законе действующих масс

Предположим, что мицеллярный комплекс одного типа находится в равновесии с мономерной формой ПАВ А\\

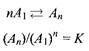
К — константа равновесия. Согласно этой модели, числа агрегации можно получить из вариации Q_ua ^ вблизи ККМ. Причем чем более плавно происходит изменение системы, тем меньше число агрегации и тем больше для описания такой системы применима модель, основанная на законе действующих масс, а не модель фазового разделения. Зависимости доли ПАВ, входящего в состав мицелл, от общей концентрации ПАВ показаны на рис. для разных чисел агрегации.

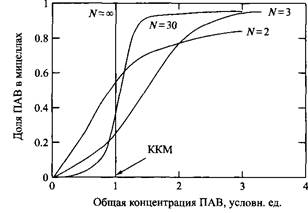
Зависимость доли ПАВ, переходящего в мицеллы, от общей концентрации ПАВ для систем с разными числами агрегации N.

При очень больших числах агрегации N на этих зависимостях наблюдается резкий скачок, и вариация в пределе будет такой же, как предсказывается моделью фазового разделения.

В реальности мицеллы не монодисперсны, поскольку всегда есть некоторое распределение по числам агрегации и мицеллы образуются постепенно, что учитывает следующая модель мицеллообразования.

4.2 Модель множественных равновесий

Данные равновесия описывают поведение неионных ПАВ. Чтобы учесть ассоциацию противоионов с мицеллами, необходимо записать равновесия для противоинов. Вообще говоря, это не совсем правильный подход, поскольку оперирование константами равновесия подразумевает взаимодействия на малых расстояниях с образованием определенных комплексов. Распределение противоионов контролируется электростатическими взаимодействиями, действующими на больших расстояниях. Именно поэтому невозможно приписать определенные характеристики противоионам, связанным с мицеллами. В то же время это не означает, что связывание противоионов или их ассоциация с мицеллой теряет физический смысл. Таким образом, необходимо представлять ограничения соответствующих моделей при анализе данных.