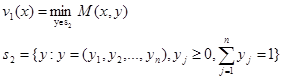Контрольная работа: Решение матричных игр
Матричной называют парную игру с нулевой суммой при условии, что каждый игрок имеет конечное число чистых стратегий.
Пусть первый игрок имеет m чистых стратегий, а второй – n .
Парная игра с нулевой суммой задается ' формально системой чисел – матрицей![]() , элементы которой определяют выигрыш первого игрока (и соответственно проигрыш второго), если первый игрок выберет i -ю строку (i -ю стратегию), а второй игрок j -й столбец (j -ю стратегию). Матрица
, элементы которой определяют выигрыш первого игрока (и соответственно проигрыш второго), если первый игрок выберет i -ю строку (i -ю стратегию), а второй игрок j -й столбец (j -ю стратегию). Матрица ![]() называется платежной матрицей или матрицей игры.
называется платежной матрицей или матрицей игры.
Задача первого игрока – максимизировать свой выигрыш.
Задача второго игрока – максимизировать свой выигрыш – сводится к минимизации проигрыша второго, что эквивалентно задаче минимизации выигрыша первого игрока.
Чистые стратегии
Гарантированный выигрыш первого игрока, применяющего чистую i -ю стратегию,
![]()
Число ![]() называется нижним значением игры, а соответствующая чистая стратегия i 0 , при которой достигается
называется нижним значением игры, а соответствующая чистая стратегия i 0 , при которой достигается ![]() называется максиминной стратегией первого игрока. Аналогично,
называется максиминной стратегией первого игрока. Аналогично, ![]() называется верхним значением игры а j 0 – минимаксной стратегией второго игрока.
называется верхним значением игры а j 0 – минимаксной стратегией второго игрока.
Всегда ![]() . Если
. Если ![]() то игра имеет седловую точку в чистых стратегиях; число
то игра имеет седловую точку в чистых стратегиях; число ![]() называется значением игры (или ценой игры ). Игра имеет седловую точку в чистых стратегиях тогда и только тогда, когда существует элемент матрицы
называется значением игры (или ценой игры ). Игра имеет седловую точку в чистых стратегиях тогда и только тогда, когда существует элемент матрицы ![]() , минимальный в своей строке и в то же время максимальный в столбце
, минимальный в своей строке и в то же время максимальный в столбце
![]()
Любая пара (i 0 , j 0 ), обладающая свойством (10.1), называется седловой точкой .
Смешанные стратегии
Если обозначить через x 1 , x 2 , …, xm вероятности (частоты), с которыми первый игрок выбирает соответственно первую, вторую, . . ., m -ю чистую стратегию, так что через ![]() ; через y 1 , y 2 , …, yn вероятности, с которыми второй игрок выбирает первую, вторую, ,.., n -ю свою чистую стратегию, причем
; через y 1 , y 2 , …, yn вероятности, с которыми второй игрок выбирает первую, вторую, ,.., n -ю свою чистую стратегию, причем ![]() , то наборы чисел x =(x 1 , x 2 , …, xm ) и y =(y 1 , y 2 , …, yn ) называются смешанными стратегиями первого и второго игроков соответственно. Каждый игрок имеет бесчисленное множество смешанных стратегий. Множество смешанных стратегий первого игрока обозначим через s 1 и множество смешанных стратегий второго игрока – через s 2 .
, то наборы чисел x =(x 1 , x 2 , …, xm ) и y =(y 1 , y 2 , …, yn ) называются смешанными стратегиями первого и второго игроков соответственно. Каждый игрок имеет бесчисленное множество смешанных стратегий. Множество смешанных стратегий первого игрока обозначим через s 1 и множество смешанных стратегий второго игрока – через s 2 .
Задача первого игрока состоит в выборе такой стратеги ![]() чтобы при отсутствии информации о выборе другого максимизировать свой выигрыш. Задача второго игрока состоит в выборе такой стратегии
чтобы при отсутствии информации о выборе другого максимизировать свой выигрыш. Задача второго игрока состоит в выборе такой стратегии ![]() , чтобы при отсутствии информации о поведении первого игрока минимизировать выигрыш первого.
, чтобы при отсутствии информации о поведении первого игрока минимизировать выигрыш первого.
Если первый игрок применяет стратегию![]() , а второй – стратегию
, а второй – стратегию![]() то средний выигрыш M (x , y )первого игрока равен
то средний выигрыш M (x , y )первого игрока равен
![]()
ВыигрышM (x , y ) называют функцией игры.
Например, в задаче с матрицей![]()
первый игрок имеет две чистые стратегии ![]() ,
, ![]() и бесчисленное множество смешанных стратегий, таких, как
и бесчисленное множество смешанных стратегий, таких, как ![]() ,
, ![]()
![]() и т. д.; все они являются элементами множества
и т. д.; все они являются элементами множества ![]() второй игрок имеет четыре чистые стратегии
второй игрок имеет четыре чистые стратегии![]() и бесчисленное множество смешанных стратегий, таких, как
и бесчисленное множество смешанных стратегий, таких, как ![]()
![]()
![]() , являющихся элементами множества
, являющихся элементами множества
![]()
Если первый игрок применяет смешанную стратегию ![]() , а второй применяет стратегию
, а второй применяет стратегию![]() , то средний выигрыш первого игрока, определяемый функцией игры, окажется равным
, то средний выигрыш первого игрока, определяемый функцией игры, окажется равным
![]()
Если же первый игрок применяет стратегию![]() , а второй — стратегию
, а второй — стратегию ![]() , то
, то ![]() . Оптимальная стратегия первого игрока
. Оптимальная стратегия первого игрока ![]() второго игрока
второго игрока![]() ;
; ![]() —цена игры.
—цена игры.
Седловая точка в смешанных стратегиях
Пара смешанных стратегий (х* , у* ) называется седловой точкой функции М (х , у ), если
![]()
Каждая матричная игра с нулевой суммой имеет решение в смешанных стратегиях, т. е. существуют такие смешанные стратегии х * и y * первого и второго игроков соответственно, что выполняется условие (10.2). Гарантированный выигрыш первого игрока, применяющего смешанную стратегию