Контрольная работа: Решение задач линейного программирования различными методами
Во втором уравнении дополнительная переменная введена с коэффициентом -1 и уравнение умножено на -1.
Постановка задачи в виде матрицы системы ограничений
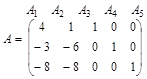
Решение задачи ЛП с составленными симплекс-таблицами
Единичные векторы A 3 , A 4 , A 5 образуют базис трехмерного пространства (m =3 ). Решать эту задачу алгоритмом симплекс-метода можно, поскольку переменные x 3 , x 4 , x 5 входят с коэффициентом +1 соответственно в первое, второе и третье ограничения. Таким образом, x 3 , x 4 , x 5 – базисные переменные, а остальные небазисные. Полагая небазисные переменные в ограничениях равными нулю, получим исходное допустимое базисное решение:
X 0 =(0,0,43,-74,76).
Заполняем исходную симплекс-таблицу (таблица 2)
Таблица 2. Нулевая симплекс-таблица
| i | Б x | Сб | A0 | - 7 | -4 | 0 | 0 | 0 | T |
| A1 | A2 | A3 | A4 | A5 | |||||
  1 | A3 | 0 | 43 |  4 | 1 | 1 | 0 | 0 |  |
| 2 | A4 | 0 | 74 | -3 | -6 | 0 | 1 | 0 | |
| 3 | A5 | 0 | 7 6 | -8 | 7 | 0 | 0 | 1 | |
| 4 | 0 | 7 | 4 | 0 | 0 | 0 |
Так как среди разностей есть положительные, то X 0 не является оптимальным решением. Строим новое базисное решение.
.
Выводим из базиса вектор A 3 ,так как
.
Разрешающий элемент таблицы x 12 выделим кругом, а разрешающий столбец и строку стрелками.
Таблица 3. Первая симплекс-таблица
| i | Б x | C б | A0 | -7 | -4 | 0 | 0 | 0 | T |
| A1 | A2 | A3 | A4 | A5 |  | ||||
 1 | A 1 | -7 |  | 1 |   | | 0 | 0 | |
| 2 | A4 | 0 |  | 0 |  |  | 1 | 0 | |
| 3 | A5 | 0 | 162 | 0 | 9 | 2 | 0 | 1 | |
| 4 |  | 0 |  |  | 0 | 0 |
Так как среди разностей есть положительные, то оптимальное решение не получено. Строим новое базисное решение.
.
Выводим из базиса вектор A 4 ,так как
.
Таблица 4. Втораясимплекс-таблица
| i | Б x | C б | A0 | -7 | - 4 | 0 | 0 | 0 | T |
| A1 | A2 | A3 | A4 | A5 | |||||
| 1 | A2 | - 4 | 43 | 4 | 1 | 4 | 0 | 0 | |
| 2 | A 4 | 0 | 736 | 21 | 0 |  | 1 | 0 | |
| 3 | A5 | 0 | -225 | -36 | 0 | -34 | 0 | 1 | |
| 4 |  | -9 | 0 |  | 0 | 0 |
Так как все разности во второй таблице (таблица 4) неположительны: 
, т получено оптимальное решение:
min (- Z )= -225.
Тогда max ( Z ) = - min (- Z ) = 225
Анализ оптимального плана.
Использование переменной x1 нецелесообразно.
Задание 3
Моделирование и решение задач ЛП на ЭВМ
Цель задания: приобрести практические навыки моделирования задач ЛП и их решения симплекс-методом с использованием прикладной программы SIMC.
Индивидуальное задание