Контрольная работа: Решение задач линейного программирования различными методами

Задание 1

Решение задач линейного программирования графическим методом

Цель задания: приобрести практические навыки решения задач линейного программирования графическим методом.

Индивидуальное задание

Найти максимум и минимум линейной формы графическим методом по исходным данным задачи ЛП (таблица 1).

Таблица 1

Номер варианта	Целевая функция	Ограничения задачи линейного программирования
6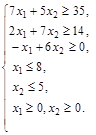

Решение задачи

Построим область L допустимых решений. Заменим в каждом неравенстве задачи знак неравенства на знак равенства. Получим уравнения прямых:

x ₁ +4x ₂ =8, 2 x ₁ - x ₂ =4, x ₁ + x ₂ ­=1, x ₁ =0, x ₂ =0.

Область L определяется как общая часть полуплоскостей, соответствующих неравенствам ограничений (рисунок 1).

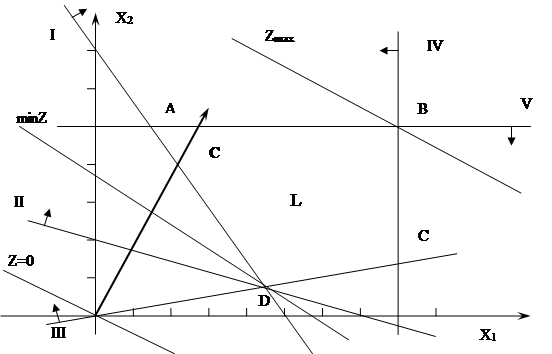Рисунок 1. Графическое решение задачи ЛП

В данной задаче она составляет многоугольник ABCD . Для нахождения экстремума функции Z =-2 x ₁ +4 x ₂ , строим разрешающую прямую, приравнивая линейную форму нулю:Z =0. Строим градиент целевой функции C(2;4).

Минимальное значение функция принимает в точке D(4,5;0,7) , а максимальное в точке B.

Анализ решения задачи линейного программирования

В результате решения задачи линейного программирования были получены минимум и максимум рассматриваемой функции, вследствие того, что область ограничений представляет собой замкнутый многоугольник, если бы фигура области ограничений была не замкнута, функция могла бы не иметь одного или обоих экстремумов в заданной области.

Задание 2

Решение задач ЛП симплексным методом с использованием симплекс-таблиц

Цель задания : закрепить теоретические сведения и приобрести практические навыки решения задач ЛП симплекс-методом.

Индивидуальное задание

Найти максимум линейной формы

Z = c ₁ x ₁ + c ₂ x ₂

при условиях:

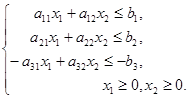
Данные представлены в таблице 2.

Номер варианта	A11	A12	A21	A22	A31	A32	B1	B2	B3	C1	C 2
6	4	1	3	6	8	7	43	74	76	7	4

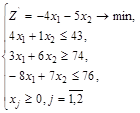
Приведем задачу ЛП к каноническому виду:

-Z’= -Z = -7x₁ -4x₂

при ограничениях

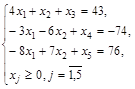
--> ЧИТАТЬ ПОЛНОСТЬЮ <--