(тыс. $)

Х1 Х2 Х3 Х4 На телевидение 1 0 0 0 1 200 На рекламные щиты 0 1 0 0 1 100 На радио 0 0 1 0 1 100 На газеты 0 0 0 1 1 100 Общие затраты на все виды реклам 1 1 1 1 4 500

Отчет по результатам

Отчет состоит из трех таблиц, расположенных на одном листе книги Excel.

Целевая ячейка (Максимум)
Ячейка	Имя		Исходное значение	Результат
$F$3	Прибыль от 1 затраченного $ Сумм-ый доход		26	3700
Изменяемые ячейки
Ячейка		Имя	Исходное значение	Результат
$B$2		План запуска рекламы Х1	1	200
$C$2		План запуска рекламы Х2	1	0
$D$2		План запуска рекламы Х3	1	200
$E$2		План запуска рекламы Х4	1	100
Ограничения
Ячейка		Имя	Значение	Формула	Статус	Разница
$F$43		Бюджет затрачиваемый на рекламу	500	$F$43<=$G$12	связанное	0
$B$2		План запуска рекламы Х1	200	$B$2<=$G$8	связанное	0
$C$2		План запуска рекламы Х2	0	$C$2<=$G$9	не связан.	100
$D$2		План запуска рекламы Х3	200	$D$2>=$G$10	не связан.	100
$E$2		План запуска рекламы Х4	100	$E$2<=$G$11	связанное	0

В первой таблице выводятся сведения о целевой функции. В столбце Исходное значение приведено значение целевой функции до начала вычислений, в столбце Результат - после оптимизации.

Следующая таблица содержит значения искомых переменных (изменяемых ячеек) до и после решения задачи.

оптимизация математическая электронная модель

Последняя таблица показывает значения левых частей ограничений на оптимальном решении задачи. В столбце Формула приведены зависимости, которые были введены в диалоговом окне Поиск решения, в столбце Разница показано количество неиспользованного ресурса. Если ресурс дефицитен, т.е. используется полностью, то в столбце Статус указывается связанное (соответствующее ограничение активно); при неполном использовании ресурса в этом столбце указывается не связанное (ограничение не активно).

Из отчета по результатам применительно к данной задаче видим, что оптимальный план распределения средств состоит в еженедельных затратах на телевидение в размере 200 000$, на газеты в размере 100 000$ и на радио в размере 200 000$, а вкладывать денежные средства в рекламные щиты не выгодно. Таким образом , и максимальный суммарный доход 000$. При этом полный бюджет на рекламу продукции используются полностью, т.е. является дефицитным, а также денежные средства отпущенные на телевидение и газеты расходуется полностью и также являются дефицитными, а денежные средства на рекламные щиты расходовать нецелесообразно.

Отчет по устойчивости

Отчет по устойчивости содержит информацию, позволяющую провести постоптимальный анализ решения задачи. Цель анализа заключается в определении таких границ изменения исходных данных задачи (коэффициентов целевой функции и правых частей ограничений), при которых ранее найденный оптимальный план сохраняет свою оптимальность и в изменившихся условиях.

Изменяемые ячейки
Результ.	Нормир.	Целевой	Допустимое	Допустимое
Ячейка	Имя		значение	стоимость	Коэффициент	Увеличение	Уменьшение
$B$2	План запуска рекламы Х1		200	5	10	1E+30	5
$C$2	План запуска рекламы Х2		0	-1	4	1	1E+30
$D$2	План запуска рекламы Х3		200	0	5	2	1
$E$2	План запуска рекламы Х4		100	2	7	1E+30	2
Ограничения
Результ.	Теневая	Ограничение	Допустимое	Допустимое
Ячейка	Имя		значение	Цена	Правая часть	Увеличение	Уменьшение
$F$43	Бюджет затрачиваемый на рекламу		500	5	500	1E+30	100

Отчет состоит из двух таблиц, расположенных на одном листе книги Excel.

В первой таблице (Изменяемые ячейки) приводится следующая информация о переменных:

· результирующее значение - оптимальные значения переменных;

· нормированная стоимость - ее величина равна значению соответствующей симплексной оценки с противоположным знаком. Для невыпускаемой продукции нормированная стоимость показывает, на сколько изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

· коэффициенты целевой функции;

· предельные значения приращения коэффициентов целевой функции, которые показывают на сколько можно увеличить и уменьшить каждый целевой коэффициент в отдельности, сохраняя при этом оптимальные значения переменных.

Во второй таблице (ограничения) приводятся аналогичные значения для ограничений задачи:

· величины использованных ресурсов (левые части ограничений) при оптимальном плане выпуска продукции;

· теневые цены, т.е. оптимальные значения двойственных переменных, которые показывают, как изменится целевая функция при изменении соответствующего запаса ресурса на единицу;

· исходные запасы ресурсов (правые части ограничений);

· предельные значения приращений ресурсов (их допустимое увеличение и уменьшение), при которых сохраняется оптимальный план двойственной задачи и базисный набор переменных, входящих в оптимальное решение исходной задачи (ассортимент выпускаемой продукции).

Используем результаты отчета по устойчивости для проведения постоптимального анализа в данной задаче:

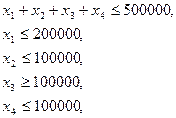
Исследуем сначала влияние на оптимальный план изменений коэффициентов целевой функции - прибыль от 1 затраченного $ на рекламу определенного вида.

Из первой таблицы следует, что оптимальный план затрат на рекламу не изменится, если первоначальная прибыль долл. рекламы Х1 возрастет на 1Е+30 доллара или уменьшится на 5 доллара. Другими словами, условие сохранения оптимального плана при изменении прибыли от рекламы Х1 имеет вид: или .

Аналогично, условие сохранения оптимального плана при изменении прибыли рекламы Х3 имеет вид: или , и условие сохранения оптимального плана при изменении прибыли рекламы Х4 имеет вид: или .

Наконец, при изменении прибыли от рекламы Х2 ранее найденный план останется оптимальным, если исходная цена возрастет не более чем на 1 доллар. В то же время любое уменьшение цены не влияет на оптимальный план , так как число равно , т.е. практически является бесконечно большим числом. Таким образом, условие сохранения оптимальности плана при изменении цены примет вид . Это означает, что рекламу Х2 не выгодно запускать (), если прибыль от нее будет не выше 5 долларов. Если же прибыль превысит 5 долларов от использования рекламных щитов, то план перестанет быть оптимальным, и в новом оптимальном решении будет положительным т.е. использование рекламы в виде рекламных щитов станет выгодным.

Отчет по пределам

Третий отчет для данной задачи, называемый отчетом по пределам, состоит из двух таблиц.

Первая таблица в комментариях не нуждается.

Целевое
Ячейка	Имя	Значение
$F$3	Прибыль от 1 затраченного $ Сумм-ый доход	3700
Изменяемое	Нижний	Целевой	Верхний	Целевой
Ячейка	Имя	Значение	предел	результат	предел	результат
$B$2	План запуска рекламы Х1	200	0	1700	200	3700
$C$2	План запуска рекламы Х2	0	0	3700	-1,15597E-09	3700
$D$2	План запуска рекламы Х3	200	100	3200	200	3700
$E$2	План запуска рекламы Х4	100	0	3000	100	3700